|
|
 发表于 24-7-2009 12:05 PM
|
显示全部楼层
发表于 24-7-2009 12:05 PM
|
显示全部楼层
回复 159# OPO 的帖子
希望你也知道,
就算不乘 1 , 5% 也可以变成 0.05的了~
之所以提出 1 的做法, 是因为 有人认为 X%一定要有个对象,
这说法才会这样出来的~
那并不是什么神奇的 1, 要反驳这个说法, 必须提出 做法有什么错误,
而不是纯粹的说它是个神奇的 1 然后笑倒在地...
请问 1x5%=0.05 又有什么错误呢? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2009 12:07 PM
|
显示全部楼层
发表于 24-7-2009 12:07 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2009 12:16 PM
|
显示全部楼层
发表于 24-7-2009 12:16 PM
|
显示全部楼层
請參考 #137
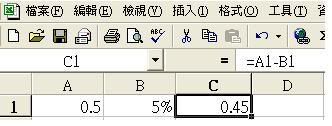 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2009 02:50 PM
|
显示全部楼层
发表于 24-7-2009 02:50 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2009 03:47 PM
|
显示全部楼层
发表于 24-7-2009 03:47 PM
|
显示全部楼层
回复 161# 飘逸手语 的帖子
Whenever we talk about a percentage, it is important to specify what it is relative to, i.e. what the total is that corresponds to 100%.
當討論 巴仙率時﹐相對的本體值很重要。
PERCENT (%) = /100 的意思﹐沒有錯。
可是 PERCENTAGE 的運用概念﹐當你用 % 時﹐ (A%) 你必須要有相對的本體值
假設﹐相對的本題值 = X
5% = 0.05 => 正確的說法是 5% of X = 0.05 of X
這個 of X, 在純數學學習時可以省略。
就好像 50% + 50% = 100% 不管 (of X) 是什麼﹐都是可以理解的。
在這裡﹐0.05 是一個比例值。不是單一存在的數值。
也只有當 0.05是比例值的情況下﹐ 5% = 0.05 才能成立。
可是﹐0.05 不一定是比例值﹐它可以是單一存在得數值。
現在回到問題﹕
0.5 - 5% = ?
0.5 可以是一個比例值 = 50% ==>主要因為是在純數學學習狀況下。
0.5﹐也可以是一個數﹐是可以單一存在的。 => 不等於 50%
如果說﹕0.5 (比例值)
0.5 (of X) - 5% (of X) = 0.45 (of X) ==> 答案等於 A (比例值)
如果說﹕0.5 (數值)
0.5 (數值) - 5% (of X) = ﹖
X = 不明數值﹐本體值。
在沒有其它數值的情況下﹐以 0.5 為本體值 ==> 答案等於 B (數值)
俺也有點亂了。。。  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2009 03:50 PM
|
显示全部楼层
发表于 24-7-2009 03:50 PM
|
显示全部楼层
回复 161# 飘逸手语 的帖子
Whenever we talk about a percentage, it is important to specify what it is relative to, i.e. what the total is that corresponds to 100%.
當討論 巴仙率時﹐相對的本體值很重要。
PERCENT (%) = /100 的意思﹐沒有錯。
可是 PERCENTAGE 的運用概念﹐當你用 % 時﹐ (A%) 你必須要有相對的本體值
假設﹐相對的本題值 = X
5% = 0.05 => 正確的說法是 5% of X = 0.05 of X
這個 of X, 在純數學學習時可以省略。
就好像 50% + 50% = 100% 不管 (of X) 是什麼﹐都是可以理解的。
在這裡﹐0.05 是一個比例值。不是單一存在的數值。
也只有當 0.05是比例值的情況下﹐ 5% = 0.05 才能成立。
可是﹐0.05 不一定是比例值﹐它可以是單一存在得數值。
現在回到問題﹕
0.5 - 5% = ?
0.5 可以是一個比例值 = 50% ==>主要因為是在純數學學習狀況下。
0.5﹐也可以是一個數﹐是可以單一存在的。 => 不等於 50%
如果說﹕0.5 (比例值)
0.5 (of X) - 5% (of X) = 0.45 (of X) ==> 答案等於 A (比例值)
如果說﹕0.5 (數值)
0.5 (數值) - 5% (of X) = ﹖
X = 不明數值﹐本體值。
在沒有其它數值的情況下﹐以 0.5 為本體值 ==> 答案等於 B (數值)
俺也有點亂了。。。  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-7-2009 12:15 AM
|
显示全部楼层
发表于 25-7-2009 12:15 AM
|
显示全部楼层
http://www.jamesbrennan.org/algebra/numbers/percents.htm
To convert a percent to a decimal
* Divide the percentage by 100 (or move the decimal point two places to the left).
Since , the decimal equivalent is just the percentage divided by 100. But dividing by 100 just causes the decimal point to shift two places to the left:
To convert a percent to a fraction
Put the percentage over a denominator of 100 and reduce
Writing a percent as a fraction is very simple if you remember that the percent is the numerator of a fraction with a denominator equal to 100.
Calculator note:
Some calculators have a percent key that essentially just divides by 100, but it can do other useful things that might save you a few keystrokes. For instance, if you need to add 5% to a number (perhaps to include the sales tax on a purchase), on most calculators you can enter the original number and then press “ + 5 % = “. Just make sure you understand what it does before you blindly trust it. What it is doing in this example is multiplying the original number by 0.05 and then adding the result onto the original number. You should be able to work any percent problem without using this key, but once you understand what is going on it can be a convenient short-cut.
如果把 percent 换去 decimal 是没有问题的,
那么我们可以做 addition 或 subtraction:
http://www.mathleague.com/help/d ... .htm#decimalnumbers
Expanded Form of a Decimal Number
The expanded form of a decimal number is the number written as the sum of its whole number and decimal place values.
Example:
3 + 0.7 + 0.06 + 0.002 is the expanded form of the number 3.762.
100 + 3 + 0.06 is the expanded form of the number 103.06.
所以这一题不应该出现 0.475 的答案。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-7-2009 10:57 AM
|
显示全部楼层
发表于 25-7-2009 10:57 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-7-2009 12:57 PM
|
显示全部楼层
原帖由 baci 于 24-7-2009 02:50 PM 发表 
楼主,你的答案是什么?  。。。 。。。
书上的答案只有一个,那就是0.45
我怕会误人子弟,因为我算到的是0.475
所以才会把这题目放上来让大家讨论,没想到竟然引起这么激烈的讨论结果。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-7-2009 12:58 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-7-2009 01:36 PM
|
显示全部楼层
发表于 25-7-2009 01:36 PM
|
显示全部楼层
To convert a percent to a decimal
* Divide the percentage by 100 (or move the decimal point two places to the left).
Since , the decimal equivalent is just the percentage divided by 100. But dividing by 100 just causes the decimal point to shift two places to the left:
To convert a percent to a fraction
Put the percentage over a denominator of 100 and reduce
Writing a percent as a fraction is very simple if you remember that the percent is the numerator of a fraction with a denominator equal to 100.
以上的解释完全正确。那只不过是在解释普通的百分比演算。
问题是到底有多少个人了解,0.5 - 5% 算出来的 0.45 是
1. 一个百分比(percentage,a fraction of some total,某一个数量的一部分,简单来说就是比率)?
2. 还是一个数量(quantity)呢?
|
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-7-2009 01:36 PM
|
显示全部楼层
发表于 25-7-2009 01:36 PM
|
显示全部楼层
在0.5 – 5%这个数学题里,出题者没有说明0.5是一个数量(quantity)还是一个百分比
(由50%演化成的0.5,也就是50% = 50/100 = 0.5)。唯一可以肯定的是,这里的5% 是一个百分比,也就是一个比率。
假设 0.5 是一个百分比,也就是一个比率。
那么这个0.5也就是一个由 50% 演算出来的 0.5 分数数值,也就是 50% =50/100 = 0.5。
这个由50%演算出来的 0.5 还是一个比率。是某一个数量的50%比率。
50%这个百分比不会通过普通数学演算而变成数量。
假设 0.5 是一个百分比,也就是一个比率。
那么这道0.5 – 5% 的数学题就变成了简单的百分比加减法而已。
也就是 0.5 – 5% = 50 / 100 – 5% = 50% - 5% = 45%
由于这只是个简单的百分比加减法,所以得出来的答案也是一个百分比。也就是说以上的 45%是一个比率。
当然你可以用简单的数学常识把它演化成 45% = 45/100 = 0.45,但请记得演化出的 0.45还是一个百分比,不是一个数量。
——————————————————————————————————————————————
假设 0.5 是一个数量呢?
就数学公式的正确写法来看,那么这道0.5 – 5% 的数学题是不合理的,是没有答案的。
为什么呢?因为这个数学题要我们从0.5 这个数量里减去一个5%。可是是什么数量的5%?
假设 0.5 是一个数量,就数学公式的正确写法来看,0.5 – 5% 还是等于0.5 – 5% 。
也就是说, 0.5 – 5% = 0.5 – 5%。因为我们无法从0.5 这个数量减去一个未知的数量。
就日常生活而言(请留意我在109#楼的论述),在看到 0.5 – 5%这个数学题时,好些人会把 0.5 当成一个数
量并且减掉里面的 0.025。 也就是 0.5 (数量)- (0.5 (数量)x 5%(百分比)) = 0.475(数量)。
用计算机算看看。得到的答案是 0.475。
因为计算机把 0.5 当成数量再减去里面的 0.025(数量)。
当然,就数学公式的正确写法来看的话,0.5 (数量) – 5% (百分比) = 0.5 (数量) – 5% (百分比)
——————————————————————————————————————————————
可是还是有人坚持,假设 0.5 是一个数量得话,我们还是可以从
0.5 – 5% = 0.5 – (1 x 5% ) = 0.5 – 0.05 = 0.45 (数量)!!!
1 x 5% = 0.05 没错啊… 绝对错不了。
在1 x 5%的数学题里,你要表达的是1这个数量的5%,所以是0.05(数量)。
也就是把1这个数量切成 100份后,拿100份里面的5份。1这个数量切成 100份后,每一份会是 0.01 (数量)。拿5份的话那么你就会有0.01 + 0.01 + 0.01+ 0.01 + 0.01 = 0.05(数量)。
可是!
问题A:在这个数学题里,没有人说这里的5%是指 1 (数量)的5%。
所以你不能够随便拿一个1 (数量) 来乘这个5%!
(结果有个很"厉害"的人为了自圆其说还在147#楼里发表了跨时代的,史无前例的数学伟论!)
问题B:有个很"厉害"的人误导大家!(大家去看110#楼)
因为那个喜欢狂嘲笑别人,很"厉害"的人连为什么什么数字值乘1都是什么数字值的概念都搞不清楚!
什么数字值乘1都是什么数字值的概念里面的1 不是一个数量!这个1是一个比率!
所以
1 (数量) x 1 (比率) = 1 (数量), 意思就是1个比率的1 (数量),就是100%的1 (数量)。答案当然就是1 (数量)!
2 (数量) x 1 (比率) = 2 (数量), 意思就是1个比率的2 (数量),就是100%的2 (数量)。答案当然就是2 (数量)!
3 (数量) x 1 (比率) = 3 (数量), 意思就是1个比率的3 (数量),就是100%的3 (数量)。答案当然就是3 (数量)!
所以以这个什么数字值乘1都是什么数字值的概念来看的话(请注意并了解这句话),
5% (百分比) x 1 (比率) = 5% (百分比), 意思就是1个比率的5% (百分比),就是100%的5% (百分比)。
答案当然还是5% (百分比)!
所以按照这个什么数字值乘1都是什么数字值的概念来看的话,
0.5 (数量) – 5% (百分比) = 0.5 (数量) – 5% (百分比)!!!
这个什么数字值乘1都是什么数字值的概念里的1根本就不是什么神奇的1可以随便的把一个百分比变成数量!
注:大家可以省省时间不用再去辩那个橙和苹果的问题然后再让自己被单位搞得晕头转向。
苹果和橙的加减的问题一开始由tingting 网友提出。里面的橙和苹果比喻的是数量和百分比,两者不能加减。
——————————————————————————————————————————————
总结:
如果假定 0.5 是百分比的话,那么对,0.5 - 5% = 50/100 - 5/100 = 45/100 = 45% = 0.45(这是百分比)。
如果假定 0.5 是数量的话,就数学公式的正确写法来看,0.5 – 5% = 0.5 – 5%
那些从
0.5 - 5% 算出来的 0.45 的网友,我希望你真的明白你算出来的0.45其实是一个百分比(percentage,
a fraction of some total,某一个数量的一部分,简单来说就是比率)
编辑原因:纠正错误编排的句子。
[ 本帖最后由 Isotope 于 25-7-2009 03:56 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-7-2009 03:25 PM
|
显示全部楼层
发表于 25-7-2009 03:25 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-7-2009 03:34 PM
|
显示全部楼层
发表于 25-7-2009 03:34 PM
|
显示全部楼层
原帖由 高曾 于 25-7-2009 12:57 PM 发表 
书上的答案只有一个,那就是0.45
我怕会误人子弟,因为我算到的是0.475
所以才会把这题目放上来让大家讨论,没想到竟然引起这么激烈的讨论结果。
很简单,
那我问你,你将给学生的答案是 A 还是 B?
如果在考试里遇到,从你的教导,
学生如果选 B ,题目的答案却是 A,
但是你觉得是 B,你将 ignore 这题目,或者还是把答案当B?。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-7-2009 03:48 PM
|
显示全部楼层
发表于 25-7-2009 03:48 PM
|
显示全部楼层
To Baci 网友,在172#楼里,为了避免我会词不达意,我一开始就注明我说的数量是 quantity
对于你对数量的解释,我不是很肯定是对是错。但肯定数量是 quantity 没错。
http://www.nciku.com/search/zh/detail/%E6%95%B0%E9%87%8F/1314179
另外按照正确的数学公式写法的话,没有人会注明单位的。只有在应用题里才会注明吧?
在172#楼里会特地强调数量而不是数字,其实道理和你说的是一样的。
数字可以是数量也可以是比率。所以当我们看到 0.5 这个数字的时候我们可以解释成数量或者是比率。
当我们看待0.5这个数字是比率时,对,0.5 - 5% = 0.45 (比率 or 百分比)
当我们看待0.5这个数字是数量时,对,0.5 - 5% = 0.5 - 5% (没有结论)
如你在173#楼里说的,不可擅自把题目的数字 0.5 数量化
我对你的回复是,不可擅自把题目的数字 0.5 百分比化
因为题目里根本没有注明0.5这个数字是数量还是百分比。
所以这个问题根本就有问题。
[ 本帖最后由 Isotope 于 25-7-2009 04:07 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-7-2009 12:47 PM
|
显示全部楼层
发表于 26-7-2009 12:47 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-7-2009 01:02 PM
|
显示全部楼层
发表于 26-7-2009 01:02 PM
|
显示全部楼层
|
以我這一代的,答案是0.475才對,那出題老師有問題嗎? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-7-2009 01:37 PM
|
显示全部楼层
发表于 26-7-2009 01:37 PM
|
显示全部楼层
原帖由 baci 于 26-7-2009 12:49 PM 发表 
我们说了这么多,不知道你同意我们说的:
"答案是不可以有 0.475 的"?。。。
如果这题目给的选择是 A) 0.45 和 B) 0.5 - 5%,
那么我们可以说题目不清楚,两个答案皆可,
但是情况不是如此。。。
你说:但是情况不是如此。。。
怎么说呢?你是要说因为这个数学题出现在小学的课业里的百分比 section 所以我们可以断定这个0.5 - 5%的数字0.5是一个比率(也就是
百分比)?如果是这样的话,我赞同你。
可是如果没有这些所谓的前提(这个数学题出现在小学的课业里的百分比 section)的话,我还是那句话:这个数学题有问题,因为它没有注明0.5这个数字是数量还是百分比。
原帖由 baci 于 26-7-2009 12:49 PM 发表 
不知道你同意我们说的:
"我们不可以把 0.5 - 5% 和 0.5 - (0.5 x 5%) 写成等式"吗?
因为这根本不应该成立的,
只不过大家把一个简单的式子口语化,
理所当然地觉得 0.5 - 5% = 0.5 - (0.5 x 5%)。。。
那些说计算机如何地得到 0.475,
就如我之前强调的,
任何计算机只不过为了 对象 而设定了 formula。。。
对计算机来说没有"数字"和"数量"的分别,
只有一种设定的 formula。。。
就正确的数学公式写法的话,对,我认同你们说的,0.5 - 5% 不代表 0.5 - (0.5 x 5%)
其实我在109#楼就那么说过了。
可是,就日常生活而言,由于问题不明确,所以很多人会直接把 0.5 - 5% 里的数字 0.5 当作数量并通过
0.5 - (0.5 x 5%) 的数学公式算出 0.475 (数量)。
最后,我还是那句话,这个问题有问题。 因为题目里根本没有注明0.5这个数字是数量还是百分比。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 27-7-2009 12:01 AM
|
显示全部楼层
发表于 27-7-2009 12:01 AM
|
显示全部楼层
请看看贴主之前的贴。
原帖由 高曾 于 13-7-2009 04:17 PM 发表 
什么出版社就不在这里写出来了。
其实书里的题目和这里有点不同,
原本的是
十分之五 - 5% =
十分之五我打不出来
5
-
10 这样又很难看。
答案 0.45
那个0.475是我自己算出来,然后在帖子上问问大 ... |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 27-7-2009 04:58 PM
|
显示全部楼层
大家争论了那么久还是没有定论。
学生给我的答案都是0.45,因为没有别的答案可以选了。
在这里大家都在原点里打转,只有一点好像是大家都认同的,那就是题目有问题。
反正在UPSR里不会出这样的题目,我也向学生表达了这样的决定。
大家要继续下去也没问题,等有定论了我再向学生认错,再给他们一个交代。
谢谢大家。 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|