【纪念当年的帖子（2010）】Add Maths功课讨论区

乙劍真人

y=(2+x)/(3-2x)

Let y=3
3=(2+x)/(3-2x)
3(3-2x)=2+x
9-6x=2+x
7x=7
x=1

so, now we know tha ...
数学神 发表于 9-2-2010 05:32 PM

u=2+x
du/dx=2 <--- du/dx = 1

接下来就 bla bla bla, ..

乙劍真人

ok
答案是 4y=-x+6

还有这题
A curve has the equation y=(x+1)^3 . Find equations of the two tangentsto the curve that is parallel to the straight line 3x-y+3 .

            y = (x+1)^3
      dy/dx = 3(x+1)^2
3(x+1)^2 = 0
  (x+1)^2 = 0
            x = -1, y = 0

当你画图的时候就找到另两条 tangent 的 point 是经过 (0,1) 及 (-2,-1)

i.e.  y-1 = 3(x-0)
         y = 3x+1

   y-(-1) = 3[x-(-2)]
         y = 3x+5

数学神

u=2+x
du/dx=2
乙劍真人 发表于 9-2-2010 20:46

都不懂自己做莫酱够力的

数学神

真人来了就好
谢谢真人指教

乙劍真人

都不懂自己做莫酱够力的
数学神 发表于 9-2-2010 09:03 PM

你一时粗心罢了啦..

superliong

y = (x+1)^3
      dy/dx = 3(x+1)^2
3(x+1)^2 = 0
  (x+1)^2 = 0
            x = -1 ...
乙劍真人 发表于 9-2-2010 08:58 PM

    請問如何找的 m ? 為什么是3？
    這題一定要用畫出來才能找到答案的嗎？

乙劍真人

請問如何找的 m ? 為什么是3？
    這題一定要用畫出來才能找到答案的嗎？
superliong 发表于 9-2-2010 09:48 PM

因为是 parallel with y = 3x+3.. 所以大家的 m 都一样..

superliong

当你画图的时候就找到另两条 tangent 的 point 是经过 (0,1) 及 (-2,-1)

这两个点如何找到？一定要画图吗？{:2_71:}

乙劍真人

回复 108# superliong

是的..暂时我只想到用图的方法，不好意思哦..

也许其他高手会进来给你其他意见吧..

walrein_lim88

回复 108# superliong


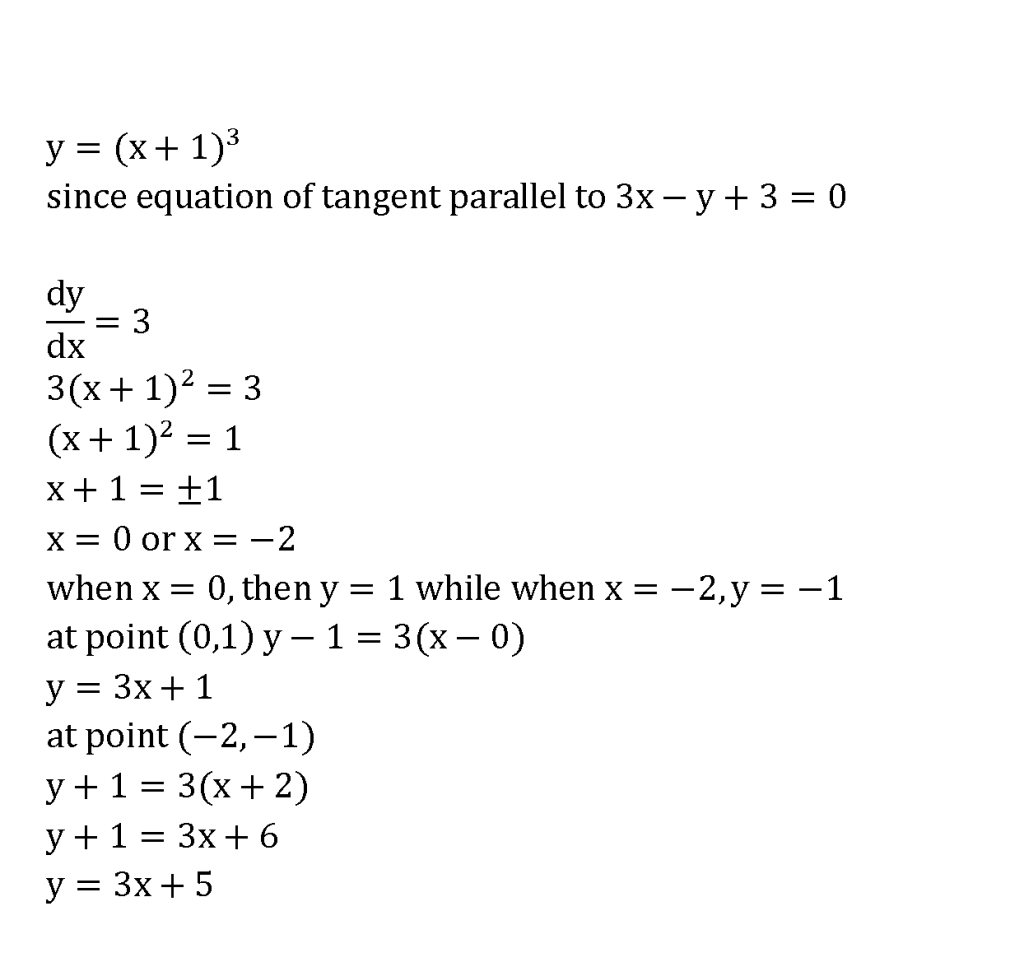
其实不用画的
记得EQUATION OF TANGENT 的 gradient=dy/dx
所以。。问题将EQUATION OF TANGENT is parallel to y=3x+3
so parallel mean same gradient
hence, dy/dx= 3
你只要DIFFERENTIATE 你的y
use dy/dx= 3，den you can find ur 2 point of tangent of the curve ald..
since tangent line is also intersect with the curve.
with the values of x, you can find ur y-coordinate using ur curve equation..

since u find out x=0 and x=-2.
sub both values of x into (x+1)^3

乙劍真人

回复  superliong


其实不用画的
记得EQUATION OF TANGENT 的 gradient=dy/dx
所以。。问题将EQUATI ...
walrein_lim88 发表于 10-2-2010 09:43 PM

对哦..怎么想不到可以利用那个 3 .. walrein 技高一筹..

walrein_lim88

对哦..怎么想不到可以利用那个 3 .. walrein 技高一筹..
乙劍真人 发表于 10-2-2010 09:48 PM

    没有啦。。。还好吧了。。
毕竟你是老师级的。，，你比较厉害。。

乙劍真人

没有啦。。。还好吧了。。
毕竟你是老师级的。，，你比较厉害。。
walrein_lim88 发表于 10-2-2010 09:49 PM

非也..我的知识也是有限的..时常在你的解答里获益良多..

walrein_lim88

非也..我的知识也是有限的..时常在你的解答里获益良多..
乙劍真人 发表于 10-2-2010 09:52 PM

Aiyerr..不要讲酱只。。。。我会害羞的。。。

superliong

两位都是高手，佩服佩服！！！！

superliong

请看看这题form 4 chapter 1 的
Given hx^2-15x+hk has root h and k , h and k cannot equal 0.
Find the possible value of h and k .

乙劍真人

请看看这题form 4 chapter 1 的
Given hx^2-15x+hk has root h and k , h and k cannot equal 0.
Find the possible value of h and k .
superliong 发表于 14-2-2010 10:45 PM

应该是 chapter 2 吧？

hx^2-15x+hk

SOR: h + k = 15/h ---(1)
POR: hk = hk/h
            = k          ---(2)

From (2), h = 1
From (1), 1 + k = 15
                    k = 14

superliong

回复 117# 乙劍真人


    抱歉，是chapter 2 的

谢谢

superliong

这两题该如何解？differentiation的
The area of a circle is increasing at the rate of 12 cm^2 s^-1 . Find the rate of increase of its radius when its circumference is 36cm .


An open cylinder has a radius of 20cm . Water is porued into the cylinder at the rate of 40cm^3s^-1 . Find the rate of increase of the height of the water level .

walrein_lim88

这两题该如何解？differentiation的
The area of a circle is increasing at the rate of 12 cm^2 s^-1 .  ...
superliong 发表于 17-2-2010 08:42 AM