|
|
 发表于 18-9-2004 06:03 PM
|
显示全部楼层
发表于 18-9-2004 06:03 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-9-2004 06:48 PM
|
显示全部楼层
发表于 20-9-2004 06:48 PM
|
显示全部楼层
想看看你们怎么证明:
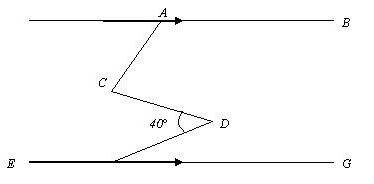
In the diagram below, thee straight line EG is parallel to AB, BAC = x°, ACD = y°, CDF = 40° and DFE = z°.
a) Show that x + y - z = 40
b) Given further that x : y : z = 7 : 3 : 8, express x in terms of z and y in terms of z.
Hence, find the value of x + y + z.
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-9-2004 11:54 PM
|
显示全部楼层
发表于 20-9-2004 11:54 PM
|
显示全部楼层
高中二高级数学
不好意思,在下的高级数学着实差了些,这儿有几题愚题,肯望各位高抬贵手,帮帮忙,恳请各位别用太深的方法来做,因为这是高中二的程度而已.
1.cari julat nilai P supaya persamaan f(x)=P mempunyai punca-punca positif sahaja diberi f(x)=2X^2-12X+9.
2.ABCD merupakan sebuah segiempat selari.A(t,0) , B(0,2t) , C(4,6) , D(t+4,6-2t) . Cari persamaan lokus bagi D dengan t berubah.
3.Sebuah silinder mempunyai isipadu yang tetap. Tunjukkan bahawa luas permukaannya adalah minimum apabila tinggi silinder itu adalah sama dengan diameter tapaknya. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-9-2004 09:59 PM
|
显示全部楼层
发表于 23-9-2004 09:59 PM
|
显示全部楼层
無聊人 于 20-9-2004 06:48 PM 说 :
想看看你们怎么证明:
In the diagram below, thee straight line EG is parallel to AB, BAC = x°, ACD = y°, CDF = 40° and DFE = z°.
a) Show that x + y - z = 40
b) Given further that x : y ...
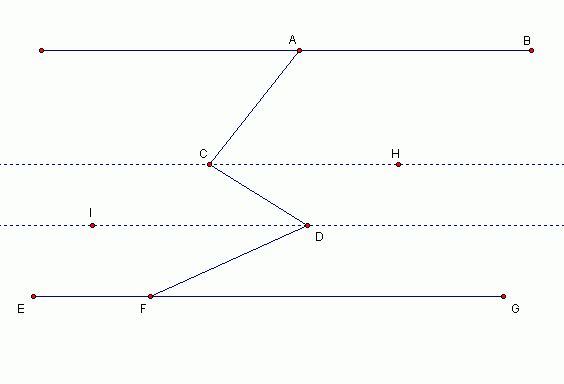
a) BAC + ACH = 180
HCD = CDI = 40 - FDI
x + y - z =180 + HCD -EFD
= 180 + HCD -(180-IDF)
= 180 + (40 - FDI) -180 + IDF
= 40
b) x/y = 7/3
y/z = 3/8
x/z = 7/8
x = 7z/8
y = 3z/8
已知
x/y = 7/3
y/z = 3/8
x/z = 7/8
代入方程 x + y - z = 40
得 x = 140
y = 60
z = 160
[ Last edited by fritlizt on 23-9-2004 at 10:07 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-9-2004 02:15 PM
|
显示全部楼层
发表于 24-9-2004 02:15 PM
|
显示全部楼层
中六难题
這是我在中六课本上遇到的一些难题,想向各位请教
由于是英文的题目,小弟不懂得翻译,请见谅
differential equation
1.A contagious disease spreads at a rate directly proportional to the product of the numberof the population infectedand the remaining population that is not infected.Initially,one-half of the population is infected and if the rate of infection is kept constant,the whole population will be infected in 24 days.Find the
proportion of the population that will be infected after 12 days.
coordinate geometry
2.Prove tat the tangent to the hyperbola xy=c^2 at the point P(cp,c/p) is p^2y+x=2cp
The perpendicular line from the origin meets this tangent at N and meets the hyperbola again at Q and R.Prove that
a)angle QPR is right angle
b)N lies on the curve (x^2+y^2)^2=4c^2xy
(解题时请附上graph)
谢谢...... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-9-2004 03:40 PM
|
显示全部楼层
发表于 25-9-2004 03:40 PM
|
显示全部楼层
Sequences And Series
这是中六数学的第三课,我完全掌握不到这一课。
请问要如何掌握这一课呢?
有关f(x)-f(x-1)的到底是怎么一回事呢?
pipi: 这问题将被移到
"中学数学讨论区-限于课业的问题 "
或许你将不懂得解答的问题提出来,让大家帮忙。。。
[ Last edited by pipi on 25-9-2004 at 09:56 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-10-2004 03:43 PM
|
显示全部楼层
发表于 6-10-2004 03:43 PM
|
显示全部楼层
[問題]-Probability
Can somebody please help me to solve problem I face in Probability.Thanks A LOT
Question 1:
In a large factory with many workers,30% of the workers belong to Union A,60% Union B and the remaining 10% does not join any union.A sample of 5 workers is selected.
(a) It is found that exactly 4 of these workers are members of unions.What is the probability that more of the members come from Union A than Union B?
(ANSWER:1/9)
Question 2:
In a sports quiz,each participant is required to answer a question,2 of which are on badminton and 3 on soccer.The questions are kept in separate envelopes.These envelopes are numbered 1 to 5 .The four participants are A,B ,C and D.They are required to pick their own questions randomly.
(a) For each of the participants,what is the probability that he will be the first to pick a question on badminton?
Question 3:
A fair tetrahedron die has four faces,each with a digit 1,2,3,and 4.The die is tossed three times.The sum of the three visible surfaces is recorded as T at each toss.The events A,B and C are defined as follows.
A=The score T at first toss is 7.
B=Sum of the first two scores is less than 15.
C=Product of the three scores is a multiple of 3.
Determine P(A),P(B),P(B│A),P(C│A),P(A U C) and P(C│A’ )
(ANSWER:1/4,3/8,1/2,3/4,15/16,11/12)
微中子:虽然是比较麻烦,不过还是请用中文发表.
pipi: 敬请留意: 这问题将被移到 "中学数学讨论区-限于课业的问题 "
http://chinese.cari.com.my/myfor ... ;page=4&fpage=1
[ Last edited by pipi on 9-10-2004 at 09:59 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-10-2004 10:33 AM
|
显示全部楼层
发表于 9-10-2004 10:33 AM
|
显示全部楼层
sample mean 問題
Q1: The standard deviation of the masses of articles in a large population is 4.55kg. Random samples of size 100 are drawn from the population. Find the probability that a sample mean will differ from population mean by less than 0.8 kg,
如何找到那個 mean呢?
Q2: Independent observation are taken from a normal distribution with mean 30 and variance 5.
Find the least value of n observations exceeds 30.5 is less than 1%
[ Last edited by lyeng on 10-10-2004 at 07:37 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-10-2004 02:10 PM
|
显示全部楼层
发表于 9-10-2004 02:10 PM
|
显示全部楼层
请帮我解答此题,
我做了好久都做不到
∫( x^3 + x^2 + 2x + 3 ) / ( x^4 + 5x^2 + 6 ) dx |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 01:31 AM
|
显示全部楼层
发表于 10-10-2004 01:31 AM
|
显示全部楼层
哇~~ 好高兴..终于可以在数学论坛里看到在我学识范围内的东西了..咳. 
Question 1:
In a large factory with many workers,30% of the workers belong to Union A,60% Union B and the remaining 10% does not join any union.A sample of 5 workers is selected.
(a) It is found that exactly 4 of these workers are members of unions.What is the probability that more of the members come from Union A than Union B?
(ANSWER:1/9)
题目里说 5 个已经有 4 个是 union 里面的人,
那么, 那个不是 union 的 10%(0.1) 就不用再算进去了.
把 union A 和 B 的 probability 转换去 100%,( 30/90 x 100% =...)
就会得到 P(union A) = 1/3, P(union B) = 2/3.
要 A 的大过 B, 4 个里面, A 不是 3 个就是 4 个.
所以用 binomial 来算, 要得到A 的可能性是..
X~B(4, 1/3)
P(X=3) + P(X=4) = 4C3(1/3)^3(2/3) + 4C4(1/3)^4
就会得到 1/9 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 01:40 AM
|
显示全部楼层
发表于 10-10-2004 01:40 AM
|
显示全部楼层
第二题没有答案, 不太敢回答..我尽量试试看好了.
Question 2:
In a sports quiz,each participant is required to answer a question,2 of which are on badminton and 3 on soccer.The questions are kept in separate envelopes.These envelopes are numbered 1 to 5 .The four participants are A,B ,C and D.They are required to pick their own questions randomly.
(a) For each of the participants,what is the probability that he will be the first to pick a question on badminton?
我把做法 expand 开来解释比较容易明白.
5 个里面有 2 个是 badminton(b), 那么如果第一个人前去, 选中了 b 的可能性是 2/5.
4 个人里面, 他要被选为第一个走过去抽的可能性是 1/4.
所以, 其中一个人要拿到的机会是 2/5 x 1/4 .
4 个人里面, 有一个会做为第二个上去抽的, 他选中 b 的可能性就已多了一点, 是 2/4.
第三个就 2/3, 第四个就 2/2.
结果就是.. 1/4 ( 2/5 + 2/4 + 2/3 + 2/2) = 0.6417 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 03:33 AM
|
显示全部楼层
发表于 10-10-2004 03:33 AM
|
显示全部楼层
这个题目看得好辛苦.. 不过还好有答案对证. 不过还好有答案对证.
Question 3:
A fair tetrahedron die has four faces,each with a digit 1,2,3,and 4.The die is tossed three times.The sum of the three visible surfaces is recorded as T at each toss.The events A,B and C are defined as follows.
A=The score T at first toss is 7.
B=Sum of the first two scores is less than 15.
C=Product of the three scores is a multiple of 3.
Determine P(A),P(B),P(B│A),P(C│A),P(A U C) and P(C│A’ )
(ANSWER:1/4,3/8,1/2,3/4,15/16,11/12)
P(A) 要丢出一个 7 来, 号码就不能重复, 所以只有 4+2+1, 没有其他的办法.
要有 4, 2, 1 向上, 只好让 3 向下了.要 3 向下的机会就是 1/4.
P(B) 要让两次加起来少过 15, 那么先看看这些..
4,3,2,1 其中三个加起来, 最小的是6, 最大的是9.
所以我要让 6,7,8,9 的其中 2 个加起来少过 15..
也只有 6+6 =12, 6+7=13, 6+8=14, 7+7=14 四种可能性.
可是不管你要丢多少出来, 每一个的可能性都只有 1/4.
所以, 6+6 的可能性是 1/4 x 1/4.,
6+7 的一样是 1/4 x 1/4, 可是这个也可以是 7+6, 所以要多算一次.
结果就是, (1/4)(1/4) + 2(1/4)(1/4) + 2(1/4)(1/4) + (1/4)(1/4) = 3/8
呼...头痛..
P(B|A), 先看看 P(B n A),
P(B) 里面, 只有 2 个算法是有 7 开始的. (i.e 7+6, 7+7)
所以就只有 (1/4)(1/4) + (1/4)(1/4) = 1/8
P(B|A) = P(B n A) / P(A) = 1/8 / 1/4 = 1/2.
P(C|A), 这题我算不到你的答案, 可是我觉得我的答案已经很完整了.
所以我怀疑你有打错还是什么的.. 如果真的是我错别鸟我..我尽力了 如果真的是我错别鸟我..我尽力了
先看看 P(C) 怎么来..
三个 6-9 的号码乘起来要能够被 3 除, 试试看就可以得到..
9 x 9 x 9 (1/4 x 1/4 x 1/4)-- 一次就好, 因为都一样.
9 x 9 x 8 3(1/4 x 1/4 x 1/4)-- 有三个可能性, 可以是 998, 989, 899.
9 x 9 x 7
9 x 9 x 6
8 x 8 x 9
8 x 8 x 6
7 x 7 x 9
7 x 7 x 6
6 x 6 x 9
6 x 6 x 8
6 x 6 x 7
6 x 6 x 6
6 x 7 x 8 6(1/4)^3 (678, 687, 786, 768, 876, 867) 六种排法
6 x 7 x 9
6 x 8 x 9
7 x 8 x 9
如此推算, 你会得到 P(C) = 7/8
好,回到 P(C|A), 在 P(C) 里, 又 7 开始的有..
7 x 7 x 9
7 x 9 x 7
7 x 7 x 6
7 x 6 x 7
7 x 9 x 9
7 x 6 x 6
7 x 8 x 9
7 x 9 x 8
7 x 6 x 8
7 x 8 x 6
7 x 6 x 9
7 x 9 x 6
一共是 12 个可能性.
所以, P(C n A) = 12(1/4)^3 = 3/16
P(C|A) = 3/16 / 1/4 = 3/4
P(A U C) = P(A) + P(C) - P(A n C)
= 1/4 + 7/8 - 3/16
= 15/16
P(C│A’ ), P(A) = 1/4, P(A') = 3/4
P(C n A'), 除了我算出来那 12 个由 7开始的可能性外, 其他的全部都不是 7开始, 所以,
一共是 56 种排法里面有 44 种不是 7 开始的, 可能性 = 44(1/4)^3 = 11/16
P(C|A') = 11/16 / 3/4
= 11/12
...注意一下发贴时间..看看我用多久算这题...  都是有人在 msn 卡卡叫叫害我的..5555... 都是有人在 msn 卡卡叫叫害我的..5555... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 04:02 AM
|
显示全部楼层
发表于 10-10-2004 04:02 AM
|
显示全部楼层
1.A contagious disease spreads at a rate directly proportional to the product of the numberof the population infectedand the remaining population that is not infected.Initially,one-half of the population is infected and if the rate of infection is kept constant,the whole population will be infected in 24 days.Find the
proportion of the population that will be infected after 12 days.
我尽量把题目简化, 可是还是有一个部分不知道怎么继续下去..
Let A = total population
a = infected.
da/dt = k(A-a)a
1/(A-a)a da = k dt
1/A [ 1/(A-a) + 1/a ] da = kt + c
1/A ln [a/(A-a)] = kt + c <-- 这个不知道有没有问题.
接下去的是, when t=0, a= 1/2 A.
substitute 进去, 会得到 c = 0.
然后我的问题就来了..可恶.
when t= 12, A=a ???
如果是这样子, k 怎么能够找?
ln (a/0) 的话是什么 ?
[ Last edited by 雨天之魂 on 10-10-2004 at 04:05 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 04:22 AM
|
显示全部楼层
发表于 10-10-2004 04:22 AM
|
显示全部楼层
∫( x^3 + x^2 + 2x + 3 ) / ( x^4 + 5x^2 + 6 ) dx
这个题目我用 integration by part 来做, 到后面会比较乱, 可是答案应该会对.
我做一半给你, 剩下的如果你不信邪还可以硬试一下.
(其实近期的 STPM 数学不会有那么难的题目.. ) )
∫( x^3 + x^2 + 2x + 3 ) / ( x^4 + 5x^2 + 6 ) dx
u = 1/(x^4 + 5x^2 + 6)
du = -(4x^3+10x)/ (x^4+5x^2+6)^2 dx
∫dv =∫ ( x^3 + x^2 + 2x + 3 ) dx
v = x^4/4 + x^3/3 + x^2 + 3x
∫( x^3 + x^2 + 2x + 3 ) / ( x^4 + 5x^2 + 6 ) dx
= uv - ∫v du
把楼上的两个部分合在一起算就有了...可是数目太多..
现在也很悃了...麻烦你自己来了.. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 08:52 AM
|
显示全部楼层
发表于 10-10-2004 08:52 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 10:44 AM
|
显示全部楼层
发表于 10-10-2004 10:44 AM
|
显示全部楼层
雨天之魂 于 10-10-2004 04:22 说 :
这个题目我用 integration by part 来做, 到后面会比较乱, 可是答案应该会对.
我做一半给你, 剩下的如果你不信邪还可以硬试一下.
(其实近期的 STPM 数学不会有那么难的题目.. ) )
∫( x^3 + x^2 + 2x + ...
怎么这样难?
好象更复杂了,
我试试看好了,
有兴趣的朋友也一起做吧,
这样一来才可以比较答案。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 10:57 AM
|
显示全部楼层
发表于 10-10-2004 10:57 AM
|
显示全部楼层
我们知道
(x^3 + x^2 + 2x + 3)/(x^4 + 5x^2 + 6) = (x ^3 + x^2 + 2x + 3)/((x^2 + 2)(x^2 + 3))
= (x(x^2 + 2) + (x^2 + 3))/((x^2 + 2)(x^2 + 3))
也就是把他换成partial fraction. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 12:28 PM
|
显示全部楼层
发表于 10-10-2004 12:28 PM
|
显示全部楼层
微中子 于 10-10-2004 10:57 说 :
我们知道
(x^3 + x^2 + 2x + 3)/(x^4 + 5x^2 + 6) = (x ^3 + x^2 + 2x + 3)/((x^2 + 2)(x^2 + 3))
= (x(x^2 + 2) + (x^2 + 3))/((x^2 + 2)(x^2 + 3))
也就是把他换成partial fraction.
昨晚神智不清, 没有想到那个做法.
好...
partial fraction 就是 lower 6 第2课后面那个部分.
(x ^3 + x^2 + 2x + 3)/((x^2 + 2)(x^2 + 3))
= Ax+B/(x^2+2) + Cx+D/(x^2+3)
= Ax^3 + 3Ax + Bx^2 + 3B + Cx^3 + 3Cx + Dx^2 + 3D
= (A+C)x^3 + (B+D)x^2 + (3A+3c)x + 3B + 3D
两边比较一下, A+C = 1, B+D = 1, 3A+3C =2 3B+3D =3.
solve 一下就可以把一个 pecahan 写成 2 个互相加/减的 pecahan了. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 02:58 PM
|
显示全部楼层
发表于 10-10-2004 02:58 PM
|
显示全部楼层
nikuang, 我尽量回答你的问题, 可是第二题我现在的课业比较少接触到, 慢点再试试.
1.cari julat nilai P supaya persamaan f(x)=P mempunyai punca-punca positif sahaja diberi f(x)=2X^2-12X+9.
2X^2-12X+9 = p
2X^2-12X+9-p =0
如果要 f(x) > 0,
那么 b^2 - 4ac > 0.
(-12)^2 - 4(2)(9-p) >0
144-72+8p >0
p > -9
3.Sebuah silinder mempunyai isipadu yang tetap. Tunjukkan bahawa luas permukaannya adalah minimum apabila tinggi silinder itu adalah sama dengan diameter tapaknya.
我找不到 3.142 的那个 symbol, 用 pi 来代替吧.
Luas permukaan silinder, L = 2 pi j^2 + 2 pi j t
如果要它 max or min, dL/dj = 0.
然后你做下去看看,
dL/dj = 4 pi j + 2 pi t.
0 = 4 pi j + 2 pi t.
-4 pi j/2 pi = t
t = - 2 j.
这个就指出当 luas 是 minimum 的时候, tinggi = 2 jejari = 1 diamter. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-10-2004 10:35 PM
|
显示全部楼层
发表于 10-10-2004 10:35 PM
|
显示全部楼层
fritlizt 于 23-9-2004 09:59 PM 说 :

a) BAC + ACH = 180
HCD = CDI = 40 - FDI
x + y - z =180 + HCD -EFD
= 180 + HCD -(180-IDF)
= 1 ...
其实还有一个更简短的方法……这不是MT问题哦! |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|