|
|
 发表于 7-11-2004 05:20 PM
|
显示全部楼层
发表于 7-11-2004 05:20 PM
|
显示全部楼层
多普勒效应 于 4-11-2004 22:58 说 :
对对!
不过,这个因式分解较难,
还有另一个方法!
希望有人贴上来 ^^
請壇主提供另一個方法
謝謝 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 7-11-2004 05:43 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-11-2004 07:18 PM
|
显示全部楼层
发表于 7-11-2004 07:18 PM
|
显示全部楼层
多普勒效应 于 7-11-2004 05:43 PM 说 :
设 a=5,两边平方得 x^4 - 2ax^2 + x + a^2 - a = 0
a^2 - (2x^2 +1)a + x^4 + x = 0
判别式 = (2x-1)^2
用公式法得 a1 = x^2 + x , a2 = x^2 - x +1
接下来的就和解法(二)一样。
[url]http://chi ...
果然是好法!
以5為主元,x為次元
構成2次方程式
[ Last edited by 灰羊 on 8-11-2004 at 01:49 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-11-2004 11:04 AM
|
显示全部楼层
发表于 8-11-2004 11:04 AM
|
显示全部楼层
sinchee 于 6-11-2004 10:24 说 :
赞同!!!!
而且,
如果 n 是自然数,
那当然包括 1,
但是,当 n =1时,
(1 + 1/n)^n = 2,并不 >2。
灰羊 于 6-11-2004 10:09 说 :
灰羊于 5-11-2004 11:00 PM 说 :
... 第一題應改成
x,y,z 都是正数
第二題鷹改成
2≤(1 + 1/n)^n <3
另外..我第二題的證法可行嗎
对不起,应是 2≤(1 + 1/n)^n <3。谢谢坛主帮我修改了。
萧晨 于 5-11-2004 22:32 说 :
大专 (C13)
证明 2< (1 + 1/n)^n <3
如果 n 是任何 自然数。
说真的,如果给我解这一题的话
我一定毫不犹豫的用画图法
首先,(1 + 1/n)^n and n is natural number
可以化为(1 + k)^(1/k) and ...
这一题,较希望网友们用 algebra 的方法解题。有一个超棒的解法,只须两行。
萧晨 于 7-11-2004 13:56 说 :
sinchee只是给了答案
我的解法对不对呀?
萧晨网友, 你的解法是对的;只是少了第一颗是要草莓机率的解法。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-11-2004 02:30 PM
|
显示全部楼层
发表于 8-11-2004 02:30 PM
|
显示全部楼层
1、連CM、DM,
則∠CMD=90度,且CM=DM,∴∠MCN=45度。
2、∵∠CMD=90度,∠CED=90度,
∴C、E、D、M四點共圓
則∠CMN=∠CDE=60度
故∠MND=∠CMN+∠MCN=105度 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-11-2004 11:53 PM
|
显示全部楼层
发表于 8-11-2004 11:53 PM
|
显示全部楼层
初中 (A38)
x=2^(2/3) + 2^(1/3) +1
(2^(1/3)-1)x=(2^(1/3)-1)(2^(2/3) + 2^(1/3) +1)=1--------->(a-1)(aa+a+1)=a^3-1
(2^(1/3)-1)=1/x
2^(1/3)=1+1/x
左右三次方-->2=(1+1/x)^3
这就是答案
[ Last edited by 萧晨 on 9-11-2004 at 01:04 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-11-2004 11:59 PM
|
显示全部楼层
发表于 8-11-2004 11:59 PM
|
显示全部楼层
大专 (C13)
证明 2 =< (1 + 1/n)^n <3
如果 n 是任何 自然数。
说真的,如果给我解这一题的话
我一定毫不犹豫的用画图法
首先,(1 + 1/n)^n and n is natural number
可以化为(1 + k)^(1/k) and 0<k<1
then draw 3 lines--->y=1+k
y=2^k
y=3^k
可以发现在0<k<1里面
y=2^k一直都在y=1+k之下---->很简单,不用画图出来也知道啦。。。(因为只有在k=0,k=1相交)
y=3^k一直都在y=1+k之上 (因为两个交点,一个是k=0,一个是k<0)
2^k=<1+k<3^k
===>2=<(1+k)^(1/k)<3 当0<k<1
===>2=<(1 + 1/n)^n<3 当n is natural number
(可以这样变换因为n is natural number 的range在0<k<1的domain里面)
当然,还是有其他的解法
证明(1+1/n)^n-2>=0,(1+1/n)^n-3<0
(1+1/n)^n-2
=[(1+n)/n]^n-2
=[(1+n)^n-2n^n]/(n^n)--------->分母先搁着一边,打字太麻烦了
=(1+n)^n-2n^n--->展开
=1+(nC1)(n)+(nC2)(n^2)+...+(nC(n-2))(n^(n-2))+(nC(n-1))(n^(n-1))+(nCn)(n^n))-2n^n
由于最后三项相加就是0-->(nC(n-1))(n^(n-1))+(nCn)(n^n))-2n^n=0
剩下的全部是正数
所以,(1+1/n)^n-2>=0
(1+1/n)^n>=2
然后就是证明(1+1/n)^n-3<0--->maximum=e<3
所以就解到了
另外一个解法y=(1+1/n)^n是一个monotonic increasing function(容易证明)
所以取最小n=1,y=2
取最大,用limit n-->无限,y=e
所以就解到了
总共有三个方法吧
可能会有更多
[ Last edited by 萧晨 on 9-11-2004 at 12:01 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-11-2004 12:11 AM
|
显示全部楼层
发表于 9-11-2004 12:11 AM
|
显示全部楼层
萧晨 于 8-11-2004 11:53 PM 说 :
初中 (A38)
x=2^(2/3) + 2^(1/2) +1
(2^(1/3)-1)x=(2^(1/3)-1)(2^(2/3) + 2^(1/2) +1)=1--------->(a-1)(aa+a+1)=a^3-1
(2^(1/3)-1)=1/x
2^(1/3)=1+1/x
左右三次方-->2=(1+1/x)^3
这就是 ...
x=2^(2/3) + 2^(1/2) +1
應該是
x=2^(2/3) + 2^(1/3) +1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-11-2004 01:05 AM
|
显示全部楼层
发表于 9-11-2004 01:05 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-11-2004 03:57 PM
|
显示全部楼层
发表于 9-11-2004 03:57 PM
|
显示全部楼层
1+1/x=(x+1)/x=〔2^(2/3) + 2^(1/3) +1+1〕/〔2^(2/3) + 2^(1/3) +1〕
=1+〔2^(1/3) -1〕(有理化分母,即分子、分母同乘以〔2^(1/3) -1〕)
=2^(1/3)
故(1+1/x)^3=2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-11-2004 08:28 PM
|
显示全部楼层
发表于 9-11-2004 08:28 PM
|
显示全部楼层
都做完了很悶吧?
給你們玩玩看...
因式分解(x+y)^7-x^7-y^7
factoring (x+y)^7-x^7-y^7
1/4=(1-a)(1-b)(1-c)
11/24=a(1-b)(1-c)+b(1-c)(1-a)+c(1-a)(1-b)
1/4=ab(1-c)+bc(1-a)+ca(1-b)
1/24=abc
解a,b,c
solve a,b,c |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-11-2004 01:41 AM
|
显示全部楼层
发表于 10-11-2004 01:41 AM
|
显示全部楼层
多普勒效应 于 31-10-2004 10:07 PM 说 :
10/11/2004,星期三
初中 (A39)
ABCD是凸四边形,且AB=BC=AC=AD,
求角BDC之值。
(待解)
(答案:)
(解对者:)
( ...
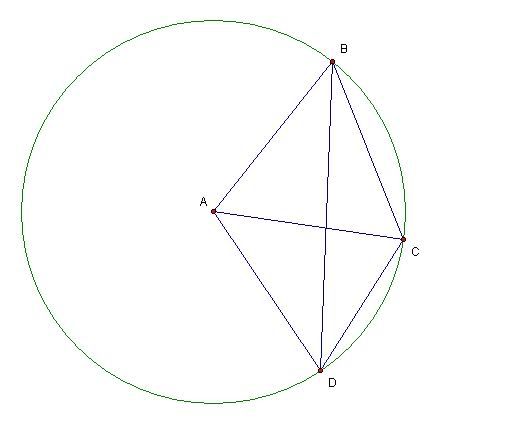
AB=BC=AC=AD,
设 角DBC 为Y, 角BDC为X.
所以, ABC为等边三角形。 内角为60度。
这四条线有一样长,可以画成圆圈。
ACD为等腰三角形。
忘了什么THEOREM, 角DAC = 2*角DBC
: 角DAC = 2Y, 焦ACD为(180-2Y)/2 = 90-Y
角BDC + 角DCA + 角ACB + 角CBD = 180
X + 90 - Y +60 + Y = 180
X + 150 = 180
X = 30.
[ Last edited by fritlizt on 10-11-2004 at 01:44 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-11-2004 03:05 AM
|
显示全部楼层
发表于 10-11-2004 03:05 AM
|
显示全部楼层
初中 (A39)
ABCD是凸四边形,且AB=BC=AC=AD,
求角BDC之值。
ABC等边三角形
ABD等腰三角形
所以可以花在一个圆圈里面
BCD在圆周
A是圆心
然后利用圆心角=2x圆周角
BAC角=2BDC角---〉以BC为底
然后就知道BDC角度是60/2=30度了
(对不起,不会用软件画图。。。) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-11-2004 09:59 AM
|
显示全部楼层
发表于 10-11-2004 09:59 AM
|
显示全部楼层
∵AB=AD
∴設∠ABD=∠ADB=a度,
則∠BAD=(180-2a)度
∵AB=BC=CA
∴∠BAC=60度
則∠CAD=∠BAD-∠BAC=(120-2a)度
∵AC=AD
則∠ADC=(180-120+2a)/2度=(30+a)度,
故∠BDC=∠ADC-∠ADB=30度 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-11-2004 11:27 AM
|
显示全部楼层
发表于 10-11-2004 11:27 AM
|
显示全部楼层
萧晨 于 6-11-2004 00:58 说 :
高中生的题目不是很难(适合我做)
大专的就。。有点难了。。难得才会一两题。。
多一些几率数学,统计学吧,
我顺便可以加强自己的能力。。。:-p
放心,不会令你失望。试试 C14 吧,在第一页。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-11-2004 04:35 PM
|
显示全部楼层
发表于 10-11-2004 04:35 PM
|
显示全部楼层
这四条线有一样长,可以画成圆圈。
===================================
其實有個名詞很適合====>共圓 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-11-2004 06:22 PM
|
显示全部楼层
发表于 10-11-2004 06:22 PM
|
显示全部楼层
flash 于 10-11-2004 11:27 AM 说 :
放心,不会令你失望。试试 C14 吧,在第一页。
pair怎么玩?
我不懂eh...可以教教一下吗?
这四条线有一样长,可以画成圆圈。
===================================
其實有個名詞很適合====>共圓
谢了,本来不懂的。

[ Last edited by fritlizt on 10-11-2004 at 06:24 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-11-2004 11:32 PM
|
显示全部楼层
灰羊 于 9-11-2004 08:28 PM 说 :
1/4=(1-a)(1-b)(1-c)
11/24=a(1-b)(1-c)+b(1-c)(1-a)+c(1-a)(1-b)
1/4=ab(1-c)+bc(1-a)+ca(1-b)
1/24=abc
解a, ...
设 a+b+c = p
ab + bc + ac = q
展开 第1 , 2 , 3式,得
q-p=-17/24 --(4)
p-2q=11/24 --(5)
q=3/8 --(6)
把 (6) 代入 (4) 或 (5)
得 p=13/12
设等式 t^3 -pt^2 + qt -1/24 = 0 的三个根为 a,b,c
通分得 24t^3 - 26t^2 +9t -1 =0
分解得 (2t-1)(4t-1)(3t-1)=0
所以 {a,b,c}={1/2 , 1/4 , 1/3} |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-11-2004 12:58 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-11-2004 08:57 AM
|
显示全部楼层
发表于 12-11-2004 08:57 AM
|
显示全部楼层
多普勒效应 于 12-11-2004 00:58 说 :
怎么星期四没人解??!!
11/11/2004,星期四
高中 (B37)
f 和 g 是两个多项式(polynomial),且
f(x + g(y))=3x + y + 4
给所有实数x,y
求 g( 8 + f (3)) 之值。
(待解)
(答案:)
(解对者:)
==========================================
有個問題,多項式是指有多個變量的式子對吧?
ax+by+cz那種 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|