|
|
【纪念当年的帖子（2008）】高級數學纲要笔记
[复制链接]
|
|
|
发表于 16-1-2010 09:12 PM
|
显示全部楼层
In an arithmetic progression,the sum of all the terms from the second term to the fourth term is 18.If the first term is 3, find the common difference.
这题我的答案是3/2，可是他的答案是negative的。请求指点......... |
|
|
|
|
|
|
|
|
|
|
|
发表于 16-1-2010 09:13 PM
|
显示全部楼层
本帖最后由 Enceladus 于 16-1-2010 09:17 PM 编辑
以上是其中三题是我在下午做的，可是就是做不出来。 |
|
|
|
|
|
|
|
|
|
|
|
发表于 16-1-2010 09:24 PM
|
显示全部楼层
我这几天被学校的的运动会搞得又忙又累，没有精神和时间去做add maths。今天做的时候，有的题目的做法忘记了 ...
Enceladus 发表于 16-1-2010 09:04 PM 
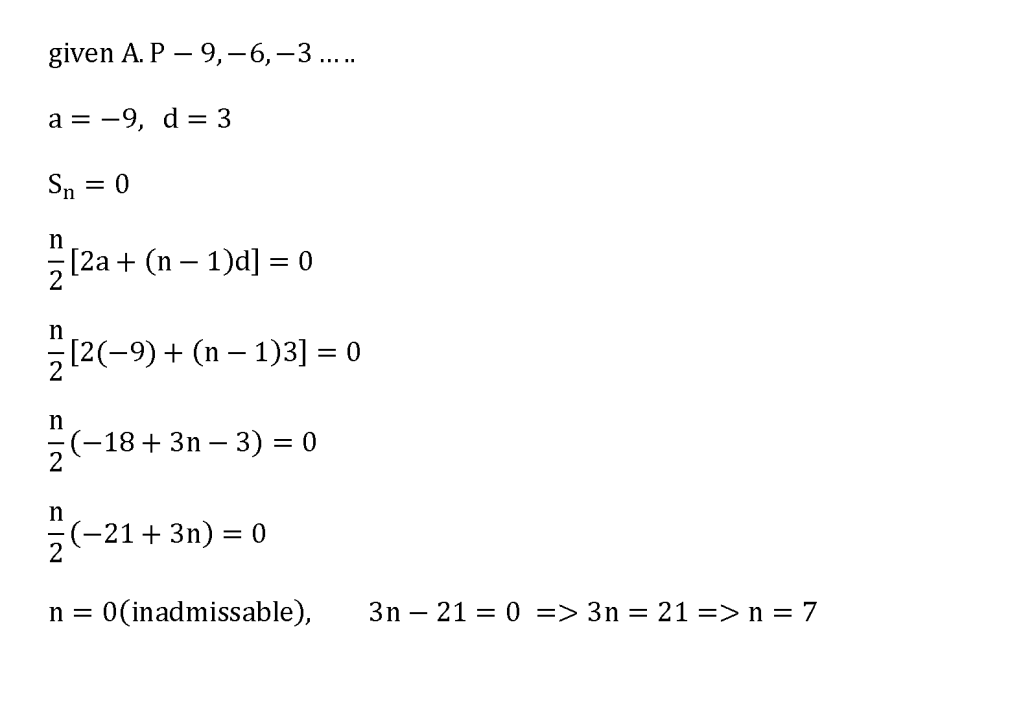
你的FORMULA应该有错，在CHECK下。 |
|
|
|
|
|
|
|
|
|
|
|
发表于 16-1-2010 09:29 PM
|
显示全部楼层
In the arithmetic progression 4,7,10...determine two consecutive terms whose sum is 65.
这题我是做 ...
Enceladus 发表于 16-1-2010 09:07 PM
 |
|
|
|
|
|
|
|
|
|
|
|
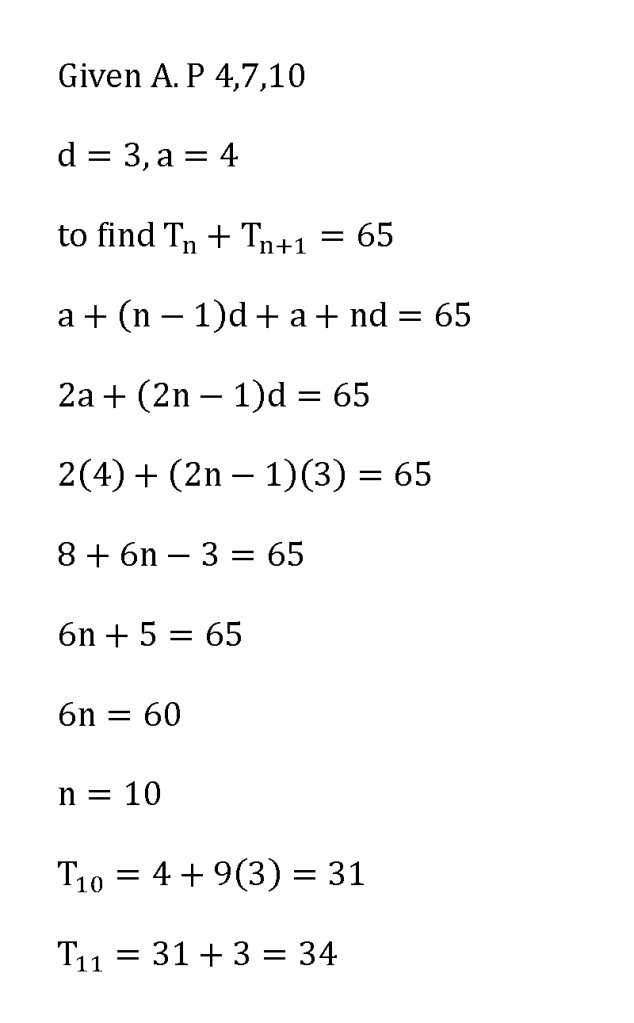发表于 16-1-2010 09:31 PM
|
显示全部楼层
|
怪不得，我没有把first term 当成9，可是他的题目没有讲-9是first term，所以我这个笨蛋就没有放进去，然后就错了。。。。。。。。。 |
|
|
|
|
|
|
|
|
|
|
|
发表于 16-1-2010 09:34 PM
|
显示全部楼层
In an arithmetic progression,the sum of all the terms from the second term to the fourth term is 18. ...
Enceladus 发表于 16-1-2010 09:12 PM
 |
|
|
|
|
|
|
|
|
|
|
|
发表于 16-1-2010 09:36 PM
|
显示全部楼层
怪不得，我没有把first term 当成9，可是他的题目没有讲-9是first term，所以我这个笨蛋就没有放进去，然后 ...
Enceladus 发表于 16-1-2010 09:31 PM
arithmetic progression-9,-6,-3 其实不清楚下。。可能没有.....,-9《=所以我当它是a了。 |
|
|
|
|
|
|
|
|
|
|
|
发表于 16-1-2010 09:37 PM
|
显示全部楼层
In an arithmetic progression,the sum of all the terms from the second term to the fourth term is 18. ...
Enceladus 发表于 16-1-2010 09:12 PM
你的答案应该没有错。。。 |
|
|
|
|
|
|
|
|
|
|
|
发表于 16-1-2010 09:55 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
发表于 19-1-2010 07:38 PM
|
显示全部楼层
真的是顶不顺，我的老师在三个礼拜内教到integration，第二课还没有消化就塞新的进来。这边有一题请你看一下。
If 3 is the third term of an AP and the sum of the first eight terms is 0,find the sum of the first fifty terms.
T^3=3
3=a+2d
S^8=0
0=8a+28d
24=8a+16d
d=-2
a=7
S^50=25(14+(49)-2)
=25(-84)
=-2100 |
|
|
|
|
|
|
|
|
|
|
|
发表于 19-1-2010 09:52 PM
|
显示全部楼层
真的是顶不顺，我的老师在三个礼拜内教到integration，第二课还没有消化就塞新的进来。这边有一题请你看一下 ...
Enceladus 发表于 19-1-2010 07:38 PM 
答案不对MEH？我也是算到这个答案。。WORKING也很好下。。。 |
|
|
|
|
|
|
|
|
|
|
|
发表于 19-1-2010 10:02 PM
|
显示全部楼层
the sum of the first n terms, Sn of a progression is given by Sn=5n-n^2, find in terms of n, the sum of the first (n-1) terms, Sn-1 then prove that in terms of n , the n^+n term,Tn of the progression and prove that the progression is an A.P
帮帮我。。。问题都看不懂了。。。没有头绪。。。 |
|
|
|
|
|
|
|
|
|
|
|
发表于 19-1-2010 10:19 PM
|
显示全部楼层
the sum of the first n terms, Sn of a progression is given by Sn=5n-n^2, find in terms of n, the sum ...
Boys_like_girls 发表于 19-1-2010 10:02 PM
 |
|
|
|
|
|
|
|
|
|
|
|
发表于 20-1-2010 09:46 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
发表于 21-1-2010 09:05 PM
|
显示全部楼层
In a geometric progression,the sum of the first five terms is 11 and the sum of the next five terms is 11/32.find the common ratio.
这题怎样做哦??帮忙我....... |
|
|
|
|
|
|
|
|
|
|
|
发表于 21-1-2010 09:45 PM
|
显示全部楼层
In a geometric progression,the sum of the first five terms is 11 and the sum of the next five terms ...
dollyeye 发表于 21-1-2010 09:05 PM 
sum of the 1st five term = T1+T2+T3+T4+T5
sum of the next five term=T6+T7+T8+T9+T10
其余，自己想想看吧。。 |
|
|
|
|
|
|
|
|
|
|
|
发表于 21-1-2010 09:55 PM
|
显示全部楼层
In a geometric progression,the sum of the first five terms is 11 and the sum of the next five terms ...
dollyeye 发表于 21-1-2010 09:05 PM
 |
|
|
|
|
|
|
|
|
|
|
|
发表于 22-1-2010 01:37 PM
|
显示全部楼层
|
In a geometric progression,the third term is 0.8 and the sum of the first two term is 7.Given that all the terms in the geometric progression are positive,find the sum of the 7th term to the 12th term |
|
|
|
|
|
|
|
|
|
|
|
发表于 22-1-2010 01:51 PM
|
显示全部楼层
In a geometric progression,the third term is 0.8 and the sum of the first two term is 7.Given that a ...
jose 发表于 22-1-2010 01:37 PM
要找两个UNKNOWN, a和r 出来，就要有2个Equation=》simulteneous
如果是GP ，就equation除 equation,如果是AP，2 equation use +/- |
|
|
|
|
|
|
|
|
|
|
|
发表于 22-1-2010 02:06 PM
|
显示全部楼层
要找两个UNKNOWN, a和r 出来，就要有2个Equation=》simulteneous
如果是GP ，就equation除 e ...
walrein_lim88 发表于 22-1-2010 01:51 PM 
a和r都找到了
the sum of 7th term to the 12th term怎样找呢？谢谢 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子
|
2118 
46
