|
|
【纪念当年的帖子(2008)】高級數學纲要笔记
 [复制链接]
[复制链接]
|
|
|
 发表于 10-1-2010 12:03 PM
|
显示全部楼层
发表于 10-1-2010 12:03 PM
|
显示全部楼层
本帖最后由 Enceladus 于 10-1-2010 12:05 PM 编辑
The first term and the last term of an arithmetic progression are -12 and 36 respectively. If the sum of all the terms of 240, find the number of terms.
这题我找不到他的common difference,做不下去了  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 12:14 PM
|
显示全部楼层
发表于 10-1-2010 12:14 PM
|
显示全部楼层
本帖最后由 walrein_lim88 于 10-1-2010 12:22 PM 编辑
The first term and the last term of an arithmetic progression are -12 and 36 respectively. If the su ...
Enceladus 发表于 10-1-2010 12:03 PM 
记得:
Sn=n/2(a+Tn) => where a=1st term Tn= last term/nth term
所以:Sn=240
n/2(-12+36)=240
n/2(24)=240
n/2=10
n=20
Sn=n/2(a+Tn) (这个基本。最Basic的)...Eq 2
Tn=a+(n-1)d ......Eq1
sub 1 into 2 :
Sn=n/2(a+a+(n-1)d)
Sn=n/2(2a+(n-1)d) <=很多人只记得这个,忘了最BASIC那个) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 12:18 PM
|
显示全部楼层
发表于 10-1-2010 12:18 PM
|
显示全部楼层
这是我刚才那题的做法:
240=n/2(-12+36)
240=n(12)
n=20
对吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 12:19 PM
|
显示全部楼层
发表于 10-1-2010 12:19 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 12:21 PM
|
显示全部楼层
发表于 10-1-2010 12:21 PM
|
显示全部楼层
这是我刚才那题的做法:
240=n/2(-12+36)
240=n(12)
n=20
对吗?
Enceladus 发表于 10-1-2010 12:18 PM 
对了。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 12:49 PM
|
显示全部楼层
发表于 10-1-2010 12:49 PM
|
显示全部楼层
这题我好像又做错了。。。。。。。
The sum of the first 6 terms of an arithmetic progression is 72 while the sum of the first 9 terms is 81. Find the common difference.
之前又做得到,现在又做不到。。。。。。。  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 12:58 PM
|
显示全部楼层
发表于 10-1-2010 12:58 PM
|
显示全部楼层
本帖最后由 walrein_lim88 于 10-1-2010 12:59 PM 编辑
这题我好像又做错了。。。。。。。
The sum of the first 6 terms of an arithmetic progression is 72 wh ...
Enceladus 发表于 10-1-2010 12:49 PM 
这题应该没问题吧。。
就做SIMULTENOUS啊
S6=72 S9=81
6/2(2a+(6-1)d)=72 9/2(2a+8d)=81
3(2a+5d)=72 2a+8d=18.......2
2a+5d=24 ....1
1-2 : -3d=6 =>d=-2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 01:10 PM
|
显示全部楼层
发表于 10-1-2010 01:10 PM
|
显示全部楼层
原来是要用simultaneous equation,我只做到这里就觉得奇怪,然后就来问你们了。
S6=72 S9=81
6/2(2a+(6-1)d)=72 9/2(2a+8d)=81
3(2a+5d)=72 2a+8d=18.......2
2a+5d=24 ....1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 01:12 PM
|
显示全部楼层
发表于 10-1-2010 01:12 PM
|
显示全部楼层
原来是要用simultaneous equation,我只做到这里就觉得奇怪,然后就来问你们了。
S6=72 ...
Enceladus 发表于 10-1-2010 01:10 PM 
记得:
看到2个UNKNOWN,就必须要有2个EQUATION=》den simultaneous
看到3个UNKNOWN, 就 3 个EQUATION=》 simultaneous (不过SPM没问到3个UNKNOWN) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 01:13 PM
|
显示全部楼层
发表于 10-1-2010 01:13 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 11:21 PM
|
显示全部楼层
发表于 10-1-2010 11:21 PM
|
显示全部楼层
我遇到一题我不会做
Given that y=x^3-3x, find the values of d'' when dy/dx=0 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-1-2010 11:32 PM
|
显示全部楼层
发表于 10-1-2010 11:32 PM
|
显示全部楼层
我遇到一题我不会做
Given that y=x^3-3x, find the values of d'' when dy/dx=0
Enceladus 发表于 10-1-2010 11:21 PM 
这一题就做两次DIFFERENTIATION
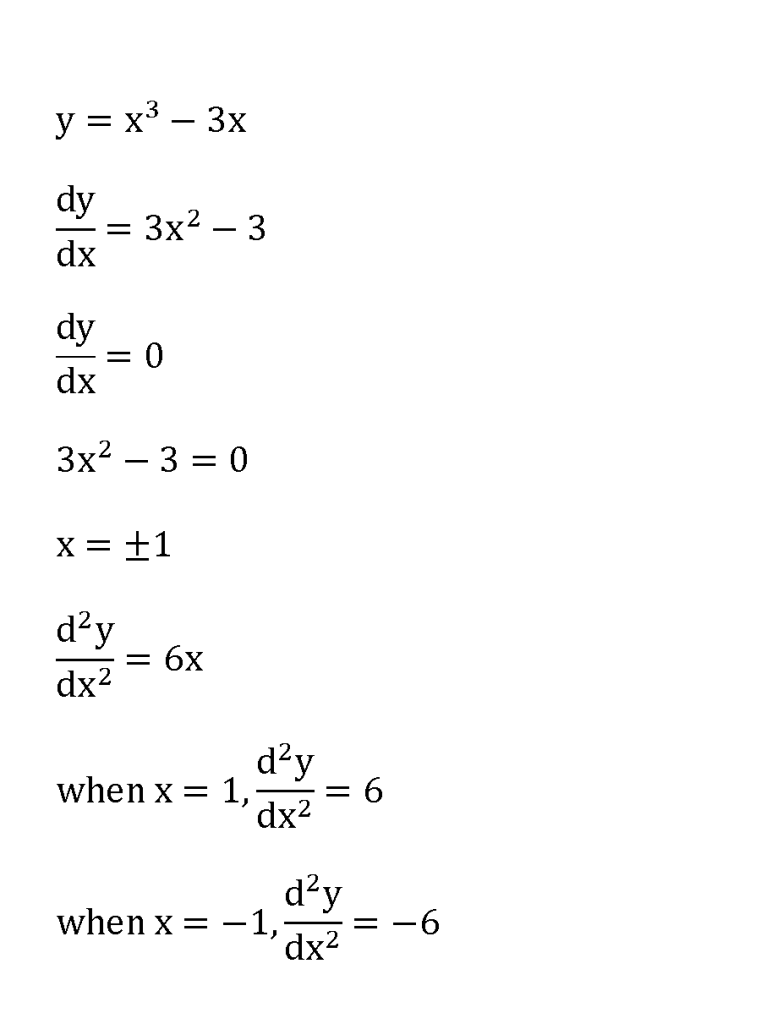 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-1-2010 12:03 AM
|
显示全部楼层
发表于 11-1-2010 12:03 AM
|
显示全部楼层
我就是做了两次的differentiation后,发现答案完全不一样,原来是这样子。可是为什么
3x^2-3=0
x=+_1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-1-2010 12:08 AM
|
显示全部楼层
发表于 11-1-2010 12:08 AM
|
显示全部楼层
我就是做了两次的differentiation后,发现答案完全不一样,原来是这样子。可是为什么
3x^2-3=0
x=+_1
Enceladus 发表于 11-1-2010 12:03 AM 
3X^2-3=0
3(X^2-1)=0
X^2-1=0
X=+-1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-1-2010 05:38 PM
|
显示全部楼层
发表于 12-1-2010 05:38 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-1-2010 05:41 PM
|
显示全部楼层
发表于 12-1-2010 05:41 PM
|
显示全部楼层
|
If y=2/t^2 and x=2t+1, find dy/dx in terms of x。这题我也是做到有点pengsan........ |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-1-2010 06:13 PM
|
显示全部楼层
发表于 12-1-2010 06:13 PM
|
显示全部楼层
If y=2/t^2 and x=2t+1, find dy/dx in terms of x。这题我也是做到有点pengsan........
Enceladus 发表于 12-1-2010 05:41 PM 
y = 2t^-2
dy/dt = -4t^-3
= -4/(t^3)
x = 2t+1
dx/dt = 2
dy/dx = dy/dt × dt/dx
= -4/(t^3) × 1/2
= -2/(t^3)
(对吗???? ) ) |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-1-2010 08:50 PM
|
显示全部楼层
If y=2/t^2 and x=2t+1, find dy/dx in terms of x。这题我也是做到有点pengsan........
Enceladus 发表于 12-1-2010 05:41 PM 
这题目必须用 chain rule..
dy/dx = dy/dt x dt/dx
y = 2/t^2 ---> dy/dt = -4/t^3
x = 2t + 1 ---> dx/dt = 2
dy/dx = dy/dt x dt/dx
= -4/t^3 x 1/2
= -2/t^3 ---(1)
Given x = 2t + 1 ---> t = (x-1)/2 ---(2)
Sub. (2) into (1),
dy/dx = -2/[(x-1)/2]^3
= -2/[(x-1)^3]/8
= -16/(x-1)^3 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2010 09:04 PM
|
显示全部楼层
发表于 16-1-2010 09:04 PM
|
显示全部楼层
我这几天被学校的的运动会搞得又忙又累,没有精神和时间去做add maths。今天做的时候,有的题目的做法忘记了,做了很久也做不出,希望可以得到各路英雄的帮忙。
Find the number of terms of the arithmetic progression-9,-6,-3...that have to be taken for the sum to be zero.
这题的答案是7,可是我做到4罢了。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2010 09:07 PM
|
显示全部楼层
发表于 16-1-2010 09:07 PM
|
显示全部楼层
In the arithmetic progression 4,7,10...determine two consecutive terms whose sum is 65.
这题我是做对了,答案是34和31,可是步骤就觉得很不对劲,希望各路英雄可以指点。 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|