|
|
 发表于 19-11-2004 12:23 AM
|
显示全部楼层
发表于 19-11-2004 12:23 AM
|
显示全部楼层
高中 (B39-2)
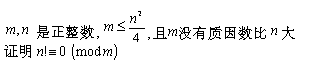
(待解)
(答案:)
(解对者:) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-12-2004 09:16 AM
|
显示全部楼层
发表于 4-12-2004 09:16 AM
|
显示全部楼层
18/11/2004,星期四
高中 (B40)
设 0<a,b<90度 , 且 sin a-sin b = -1/3
cos a - cos b= (2√2) /3
证明 b - a =60度
(已解)
(答案:)
(解对者:sinchee)
解法
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-12-2004 09:19 AM
|
显示全部楼层
发表于 4-12-2004 09:19 AM
|
显示全部楼层
19/11/2004,星期五
高中 (B41)
N 是一个正整数,求最小的 N使 N^2 的末尾四数为 6004
(已解)
(答案:998)
(解对者:sinchee,430201)
解法(一)
設N的末尾二數為B,其餘為A
則N=100A+B
N^2=10000A^2+2×100A×B+B^2-----(1)
即2×100A×B+B^2的末尾四數為6004
B^2的末二位數為04
設B=(ab),顯然b=2或8
一)若b=2
B^2=100a^2+40a+4
得a=0或5
1)a=0→B=02,
則2×100A×B+B^2=400A+4
即400A的末尾四數為6000
可得A的尾數為0或5
若A的尾數為0,得A的最小值為40;
若A的尾數為5,得A的最小值為15。
2)a=5→B=52,
則2×100A×B+B^2=10400A+2704
即10400A的末尾四數為3300
但4的倍數的尾數不可能為3,故無解。
二)若b=8
B^2=100a^2+160a+64
得a=4或9
1)a=4→B=48,
則2×100A×B+B^2=9600A+2304
即9600A的末尾四數為3700
但6的倍數的尾數不可能為7,故無解。
2)a=9→B=98,
則2×100A×B+B^2=19600A+96044
即19600A的末尾四數為6400
可得A的尾數為4或9
若A的尾數為4,得A的最小值為34;
若A的尾數為9,得A的最小值為9。
綜上所述,故最小的N為998
解法(二)
因为 N^2 的末尾数为 4,
所以 N = 10A ± 2
N^2 = 100A^2 ± 40A + 4
又,因为 N^2 的百位数字为 0,
故得知 A 的末尾数必须是 0,
因此,N 可以写成 100B ± 2,
N^2 = 10000B^2 ± 400B + 4
要使千位数字为 6,
则 ± 400B 必须是 +...6000 或 -...4000。
即 B = 15,65,... 或 10,60,...
由此可见,N 的最小值为 100(10)-2,即998。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-12-2004 09:20 AM
|
显示全部楼层
发表于 4-12-2004 09:20 AM
|
显示全部楼层
20/11/2004,星期六
高中 (B42)
(abc)是一个三位数,问共有几个这样的三位数使 a≤b≤c.
(已解)
(答案:165)
(解对者:430201)
(1)a=1,b=1,c=1~9
a=1,b=2,c=2~9
----------
a=1,b=9,c=9
共:9+8+7+…+1=45(個)
(2)a=2,b=2,c=2~9
a=2,b=3,c=3~9
----------
a=2,b=9,c=9
共:8+7+6-…+1=35(個)
-------------
(8)a=8,b=8,c=8、9
a=8,b=9,c=9
共:2+1=3(個)
(9)a=9,b=9,c=9
共:1(個)
合計=45+36+28+21+15+10+6+3+1=165(個 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-12-2004 09:21 AM
|
显示全部楼层
发表于 4-12-2004 09:21 AM
|
显示全部楼层
25/11/2004,星期四
高中 (B43)
解联立方程:
X_i 是实数
X_1 + X_2 + ... + X_1999 = 1999
(X_1)^4 + (X_2)^4 + ... + (X_1999)^4 = (X_1)^3 + (X_2)^3 + ... + (X_1999)^3
(待解)
(答案:)
(解对者:) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-12-2004 09:22 AM
|
显示全部楼层
发表于 4-12-2004 09:22 AM
|
显示全部楼层
26/11/2004,星期五
高中 (B44)
a_i 是正整数 i=1,2,3,...,n
已知 a_1 + a_2 + ... + a_n = 2002
求 (a_1)(a_2)...(a_n)的最大值。
(待解)
(答案:)
(解对者:) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-12-2004 09:23 AM
|
显示全部楼层
发表于 4-12-2004 09:23 AM
|
显示全部楼层
27/11/2004,星期六
高中 (B45)
i,j是正整数,
当 i,j 属于 S ,则 (i+j)/gcd(i,j) 属于 S
找出所有有限非空集 S
[ gcd(a,b) 表示 a,b 的最大公因数 ]
(待解)
(答案:)
(解对者:) |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|