|
|
 发表于 23-8-2004 02:46 AM
|
显示全部楼层
发表于 23-8-2004 02:46 AM
|
显示全部楼层
今天就来一个vector的问题吧。
Find the equation for the line L of intersection of the plane 3x+2y-4z-6 = 0 and x-3y-2z-4 = 0. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-8-2004 09:01 AM
|
显示全部楼层
发表于 23-8-2004 09:01 AM
|
显示全部楼层
fritlizt 于 23-8-2004 02:36 AM 说 :
想问一下, 1/(1+x) = 1-x+x^2-x^3+x^4...........这个式子是怎样来的。
书本上有解释,不过我不太明白。
]
1/(1+x) = 1-x+x^2-x^3+x^4-... 这个式子 valid 如果|x|<1 。
要证明它,有两个方法:
(一)用 binomial theorem
(二)用 geometry progression (janjang geometri)
试试看!! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-8-2004 10:05 PM
|
显示全部楼层
发表于 24-8-2004 10:05 PM
|
显示全部楼层
fritlizt 于 23-8-2004 02:36 AM 说 :
想问一下, 1/(1+x) = 1-x+x^2-x^3+x^4...........这个式子是怎样来的。
书本上有解释,不过我不太明白。
[ Last edited by fritlizt on 23-8-2004 at 02:38 AM ]
直接用长除法 (long division) 亦可,当然仍须注意 |x|<1
[ Last edited by yaahoo on 24-8-2004 at 10:06 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-8-2004 01:07 AM
|
显示全部楼层
发表于 25-8-2004 01:07 AM
|
显示全部楼层
这样的话,可不可以帮我找出 1/(1-x) 的 series?
能的话,把step 都post上来,作为参考之用。 谢谢。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-8-2004 09:40 AM
|
显示全部楼层
发表于 25-8-2004 09:40 AM
|
显示全部楼层
fritlizt 于 25-8-2004 01:07 AM 说 :
这样的话,可不可以帮我找出 1/(1-x) 的 series?
能的话,把step 都post上来,作为参考之用。 谢谢。
假设你已了解
1/(1+x) = 1-x+x^2-x^3+x^4-... , |x|<1
那么
1/(1-x) = 1/(1+(-x))
= 1 - (-x) + (-x)^2 - (-x)^3 + (-x)^4 -... , |-x|<1
= 1 + x + x^2 + x^3 + x^4 + ... , |x|<1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-8-2004 11:47 AM
|
显示全部楼层
发表于 28-8-2004 11:47 AM
|
显示全部楼层
fritlizt 于 23-8-2004 02:46 AM 说 :
今天就来一个vector的问题吧。
Find the equation for the line L of intersection of the plane 3x+2y-4z-6 = 0 and x-3y-2z-4 = 0.
This question can be solved by Gaussian elimination.
The augmented matrix, [3, 2, -4, 6; 1, -3, -2, 4] equivalent to [1, 0, -16/11, 26/11; 0, 1, 2/11, -6/11].
Hence, the solution (i.e. all the points that form the line L) is:
[26/11; -6/11; 0] + t[16/11; -2/11; 1] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 4-9-2004 01:45 AM
|
显示全部楼层
fadeev_popov 于 28-8-2004 11:47 说 :
This question can be solved by Gaussian elimination.
The augmented matrix, [3, 2, -4, 6; 1, -3, -2, 4] equivalent to [1, 0, -16/11, 26/11; 0, 1, 2/11, -6/11].
Hence, the solution (i.e. all the ...
这个方法可行,很赞。同时也借此机会向大家解释这题:
这题主要寻找直线方程 就是 L= a+tb a为直线上的向量,b为单位向量。根据题意:该直线与两个plane相交,首先我们要找出 normal of plane 3x+2y-4z-6 = 0 and x-3y-2z-4 = 0. 。
设 normal of plane 3x+2y-4z-6 = 0 为 n1, n1=(3,2,-4)
normal of plane x-3y-2z-4 = 0 为 n1, n1=(1,-3,-2)
用 cross product n1 * n2= -16 i + 2j -11k
b的向量为 n1*n2= -16i+2j-11k
接着就是找a的向量, 利用任何的消元法求 x,y,z的值
3x+2y-4z=6 ---(1)
x-3y-2z=4 ---(2)
设 z=0 得到, x=26/11, y=-6/11
a的向量为 26/11i-6/11k
所得的直线方程为 L=(26/11,-6/11,0)+t(-16,2,-11) |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 4-9-2004 02:40 AM
|
显示全部楼层
4/9/2004 今天来一题比较接近工程的题目
今天来一个生动的复数题目,是一个电路图,不需要用复杂的电子知识。

根据上图所示的电路图,求电动势VAB的值。
注意:1.1071是弧度
[ Last edited by 辉文 on 4-9-2004 at 02:55 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-9-2004 11:32 AM
|
显示全部楼层
发表于 4-9-2004 11:32 AM
|
显示全部楼层
Let P = 10, Q = -15j, R = 4.4721|-1.1071, S = 3+j4, T = 16, U = 8+j8, V = 12
V_A = ((P//Q)/((P//Q)+R))*V
V_B = (S/(S+(T//U)))*V
where X//Y = X*Y/(X+Y)
V_AB = V_A - V_B
Not sure correct or not  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-9-2004 12:28 AM
|
显示全部楼层
发表于 24-9-2004 12:28 AM
|
显示全部楼层
我得idea也是这样。
算出来的结果为 1.472-3.14i V
好像有点怪怪。。。。
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-9-2004 09:16 PM
|
显示全部楼层
发表于 29-9-2004 09:16 PM
|
显示全部楼层
玩玩这题吧。
答案在我们朋友之中还蛮具有争论性的 。
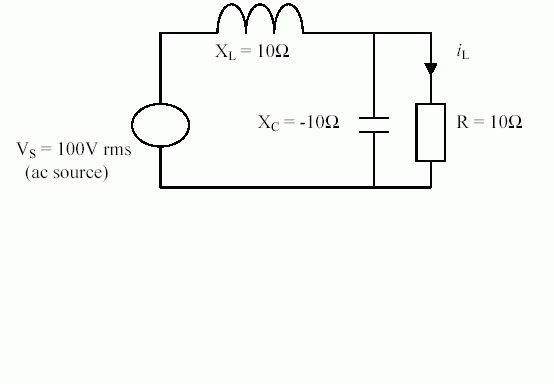
iL =??
其实这题的解法在数学里是行不通的。
想看看各位的对这题有什么看法。
[ Last edited by fritlizt on 29-9-2004 at 09:19 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-10-2004 02:36 PM
|
显示全部楼层
发表于 1-10-2004 02:36 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-10-2004 12:50 PM
|
显示全部楼层
发表于 6-10-2004 12:50 PM
|
显示全部楼层
eeCyang 于 1-10-2004 02:36 PM 说 :
我是个freshman in elecronic engineering..
不好意思...请问Xc为什么有-ve value的??? 
:sp:我觉得 iL 是不定的..(由于是ac voltage)
Vin会一直改变...如果要的话可以找imax,i(when V=x)...
...
图中XL 及 Xc 分别指他们的reactance, 也就是说只取impedence的imaginary part.
已知inductor的impedence是 jWL, XL就是指WL,
所以他的impedence是jWL , reactance是 WL。
j是虚数。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-10-2004 05:27 PM
|
显示全部楼层
发表于 6-10-2004 05:27 PM
|
显示全部楼层
fritlizt 于 29-9-2004 09:16 PM 说 :
玩玩这题吧。
答案在我们朋友之中还蛮具有争论性的 。

iL =??
其实这题的解法在数学里是行不通的。
想看看各位的对这题有 ...
答案是否:
iL = 0.997+j0.995 ?? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-10-2004 06:12 PM
|
显示全部楼层
发表于 6-10-2004 06:12 PM
|
显示全部楼层
chmwai 于 6-10-2004 05:27 PM 说 :
答案是否:
iL = 0.997+j0.995 ??
可不可以连做法都一起post上来阿? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-10-2004 08:31 AM
|
显示全部楼层
发表于 7-10-2004 08:31 AM
|
显示全部楼层
fritlizt 于 6-10-2004 06:12 PM 说 :
可不可以连做法都一起post上来阿?
很抱歉,之前的方案错了。现在再来试试。。。
首先找出电容与电阻的总电阻:
1/[(1/10)-j10]
=1/[(1-j100)/10]
=10/(1-j100)
=0.1<89.43
then,总电阻:
10/(1-j100) + j10
=[10+j10+j^2(1000)]/(1-j100)
=(1010+j100)/(1-j100)
=(1014.9<5.65)/(100<-89.42)
=10.149<95.07
然后用ratio找出电阻的电压:
(0.1<89.43)/(10.149<95.07) x 100
=0.00985<-5.64 V
then,
iL = (0.00985<-5.64)/10
= 0.000985<5.64 A
可是答案怪怪的。。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-10-2004 09:32 AM
|
显示全部楼层
发表于 7-10-2004 09:32 AM
|
显示全部楼层
chmwai 于 7-10-2004 08:31 AM 说 :
很抱歉,之前的方案错了。现在再来试试。。。
首先找出电容与电阻的总电阻:
1/[(1/10)-j10]
=1/[(1-j100)/10]
=10/(1-j100)
=0.1<89.43
then,总电阻:
10/(1-j100) + j10
=[10+j10+j^2(100 ...
好像不对。
嗯。。试用thevenin theorem来做。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-10-2004 11:20 AM
|
显示全部楼层
发表于 7-10-2004 11:20 AM
|
显示全部楼层
fritlizt 于 7-10-2004 09:32 AM 说 :
好像不对。
嗯。。试用thevenin theorem来做。
thevenin theorem?让我想一想,毕业都好几年了,差不多都还给老师了。
拿电阻作为参考点,short掉voltage source,算出XL&XC的总电阻先,再加上R,就拿到全部的电阻,最后用 Ohm's Law 算出IL,对吗?
XL // XC
=1/[(1/j10)-(j10)]
=(j10)/(1-j^2 100)
=j10/101
XL // XC + R
=j10/101 + 10
=10<0.567
IL = 100/(10<0.567)
= 10<-0.567 A |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-10-2004 07:03 PM
|
显示全部楼层
发表于 7-10-2004 07:03 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-10-2004 09:56 PM
|
显示全部楼层
发表于 7-10-2004 09:56 PM
|
显示全部楼层
微中子 于 7-10-2004 07:03 PM 说 :
这些问题在工程系里当作是数学?
没有。只是做法有点怪。
在数学来讲好像不可以。
所以post上来讨论一下。
等下post他的solution上来。 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|