|
|
最近在读着 "Mathematical Olympiad Challenges" 这本书,
里面有提到一个技巧:
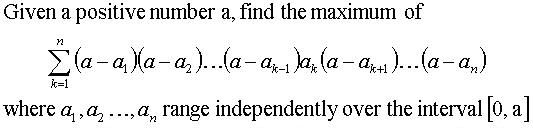
For an index k, fix a1,a2,...,ak-1,ak+1,...,an, and think of the given expression as a function in ak. This function is linear, hence its maximum on the interval [0,a] is attained at one of the endpoints. Repeating the argument for each variable, we conclude that the expression reaches its maximum for a certain choice of ak = 0 or a, k = 1,2,...,n.
If all ak's are equal to 0, or if two or more ak's are equal to a, the sum is 0. If one ak is a and the others are 0, the expression is equal to a^n; hence this is the desired maximum.
我觉得这个论证(上色那句)很不严谨。
有没有可能存在某一个数,使得这个表达式的值大于a^n,这点并没有很完整地被证明。
大家有什么看法?
[ 本帖最后由 Ivanlsy 于 20-11-2009 02:03 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-11-2009 03:06 PM
|
显示全部楼层
发表于 20-11-2009 03:06 PM
|
显示全部楼层
"有没有可能存在某一个数,使得这个表达式的值大于a^n"
不可能, 因为
a - a_i =< a for any 1 =< i =< n |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-11-2009 08:15 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 20-11-2009 03:06 PM 发表 
"有没有可能存在某一个数,使得这个表达式的值大于a^n"
不可能, 因为
a - a_i =< a for any 1 =< i =< n
要注意到是sum。
对于任意一个k,是不会大于a^n,如果是总和就不一定了。
[ 本帖最后由 Ivanlsy 于 20-11-2009 08:31 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-11-2009 10:39 PM
|
显示全部楼层
发表于 20-11-2009 10:39 PM
|
显示全部楼层
回复 3# Ivanlsy 的帖子
看错,不好意思
但他的 argument 没问题
那个 sum 的 expression 写法有一点错误,不过假设就如我们想的。
假设那个 sum with fix index k, S_k = f(a_k)
那么 f(a_k) 是一个 linear function 所以 max 在 a_k = 0 or a_k = a ,就只有两个可能性 for all k .
就因为这样,我们才可以说 repeat the argument for all k, 因为上面的句子“ f(a_k) 是一个 linear function ” is true for all k |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 21-11-2009 12:03 AM
|
显示全部楼层
原帖由 dunwan2tellu 于 20-11-2009 10:39 PM 发表 
看错,不好意思
但他的 argument 没问题
那个 sum 的 expression 写法有一点错误,不过假设就如我们想的。
假设那个 sum with fix index k, S_k = f(a_k)
那么 f(a_k) 是一个 linear function 所以 max ...
你想的sum是怎样?
也就是说题目表达方式有问题? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-11-2009 01:24 PM
|
显示全部楼层
发表于 21-11-2009 01:24 PM
|
显示全部楼层
|
a1(a-a2)(a-a3)...(a-an) + (a-a1)a2(a-a3)..(a-an) + (a-a1)(a-a2)a3(a-a4)...(a-an) + ... (a-a1)(a-a2)....(a-a_(n-1))an |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 21-11-2009 11:00 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 20-11-2009 10:39 PM 发表 
看错,不好意思
但他的 argument 没问题
那个 sum 的 expression 写法有一点错误,不过假设就如我们想的。
假设那个 sum with fix index k, S_k = f(a_k)
那么 f(a_k) 是一个 linear function 所以 max ...
令f(ak) = (a - a1)(a - a2)...(a - ak - 1)ak(a - ak + 1)...(a - an)
设k = 1,且a2, a3, ... , an为任意定值。
当a1 = a 或 0时,f(a1)是极大值。
可是这不能保证f(a2)也会是极大值,
“说不定”a1 = a 或 0 会导致f(a2)是极小值?
如果真的发生这样的情况,
会不会存在某一个a1值,
使得f(a1) + f(a2) 大于原先a1 = a or 0 时的f(a1) + f(a2)? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-11-2009 11:43 AM
|
显示全部楼层
发表于 22-11-2009 11:43 AM
|
显示全部楼层
我做了一下计算
可能的极值点应该是
a_1=a_2=a_3=...=a/n
极值是
a^n((n-1)/n)^(n-1)
不知道对不对 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-11-2009 03:16 PM
|
显示全部楼层
发表于 22-11-2009 03:16 PM
|
显示全部楼层
|
对,可是(n-1)/n<1, ==> ((n-1)/n)^(n-1)<1,所以还是不能大于a^n。我证到了所有a_1=a_2=a_3=...=a/t, t=any number greater than 1 都不可能让那个sum 大过a^n。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 22-11-2009 08:05 PM
|
显示全部楼层
原帖由 puangenlun 于 22-11-2009 11:43 AM 发表 
我做了一下计算
可能的极值点应该是
a_1=a_2=a_3=...=a/n
极值是
a^n((n-1)/n)^(n-1)
不知道对不对 原帖由 antimatter 于 22-11-2009 03:16 PM 发表 
对,可是(n-1)/n ((n-1)/n)^(n-1)
你们是通过软件计算的吗?
能不能提出进一步的证明呢? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-11-2009 09:33 PM
|
显示全部楼层
发表于 22-11-2009 09:33 PM
|
显示全部楼层
我是将sum看成是a_1,...,a_n的function
然后做∂y/∂a_i
并且令∂y/∂a_i=0
得到n个方程,解这个方程组
算到a_1=...=a_n=a/n
问题是:我不确定这个是不是极值点 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-11-2009 10:38 PM
|
显示全部楼层
发表于 22-11-2009 10:38 PM
|
显示全部楼层
我的很简单,把a/t 代进那个sum,然后differentiate 再等于零,找到的是t = n+1,可是a^n 的coefficient 还是小于1。
我用电脑软件画出了n=2, a=5 的curve,证实如果是n=2 的话,a1=0, a2=1 or a1=1, a2=0 是最大的值。
Puangenlun,原来你是那样做的啊,可是那个方程组不是很多很长吗?看了你的答案我有想到这个方法,可是好像很恐怖,所以我只做n=2 的,结果是a1=a2=a/2。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-11-2009 12:46 AM
|
显示全部楼层
发表于 23-11-2009 12:46 AM
|
显示全部楼层
回复 7# Ivanlsy 的帖子
不会,因为 a1,a2...,an 是 independent 的。
我拿一个比较小的例子 n = 2
S = a1(a-a2) + (a-a1)a2
当 a2 fix 时候,你会看到 S 是一个 linear function of a1, 而且我们知道 linear function max 在 endpoint.
注意到这里我们说 a2 是 fix ,但是其实他是 arbitrary 的。也就是说不论 a2 是什么fix number,我们要 maximise 的 a1 还是锁定在 end point.
所以整个sum的 maximum一定当 ai 都在 end point 时候
@puangenlun
a1=a2=a3=...a=n= a/n 只不过是一个 turning point, 不是任何 critical point. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-11-2009 01:27 PM
|
显示全部楼层
发表于 23-11-2009 01:27 PM
|
显示全部楼层
antimatter, 可以看看你的图吗?
dunwan2tellu,你是怎样知道这是turning point 而不是critical point的?这个turning point有什么意义/含义? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-11-2009 02:12 PM
|
显示全部楼层
发表于 23-11-2009 02:12 PM
|
显示全部楼层
回复 14# puangenlun 的帖子
你用的方式是 Langrange Multiplier method 来找 max min, 但是这方式还要配合找 boundary point 才能比较 max min.
为何是 turning point? 不就因为 ∂y/∂a_i=0 for all i |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-11-2009 08:30 PM
|
显示全部楼层
发表于 23-11-2009 08:30 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-11-2009 07:58 PM
|
显示全部楼层
发表于 25-11-2009 07:58 PM
|
显示全部楼层

这是n=2, a=5;axis 是a1, a2 和 sum。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-11-2009 01:17 AM
|
显示全部楼层
发表于 26-11-2009 01:17 AM
|
显示全部楼层
这个图很有考察意义
只是图形是立体的
在论坛的平面上很难看清楚 看明白
能不能把它转换成平面的,带有colour bar 的那一种
会比较容易看清楚
【我还在找matlab来download,否则可以亲自做来看看】 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-11-2009 10:00 AM
|
显示全部楼层
发表于 26-11-2009 10:00 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-11-2009 04:01 PM
|
显示全部楼层
发表于 26-11-2009 04:01 PM
|
显示全部楼层
这张图很有意义,它让我明白(a/2,a/2)这个 critical point 在这里的意思
在 x∈ [0,a] 上截出线段(x,0)-(x,a),就可以发现到
x∈ [0,a/2] 时,max(f)=f(x,a)∈ [a^2/2,a^n]
x=a/2时, f(x,y)=a^2/2 是 constant
x∈ [0,a] 时,max(f)=f(x,0)∈ [0,a^2/2]
同理,对于 y-axis 也有类似的结论
看了n=3的形式
x(a-y)(a-z)+(a-x)y(a-z)+(a-x)(a-y)z=a^2(x+y+z)-2(xy+yz+zx)+3xyz
我猜想f(x,y,z)的极大值点应该是(a,0,0),(0,a,0),(0,0,a)
极大值为a^3
更一般地
f(a_1,...,a_n)有n个极大值点,分别是(a,0,...,0),... ...,(0,...,0,a)
极大值为a^n
这样需要证明f<=a^n
期待各位接力
[ 本帖最后由 puangenlun 于 26-11-2009 04:04 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|