|
查看: 1429|回复: 8
|
integral(8&4) y dy/(y^2-2y-3)
[复制链接]
|
|
|
想问问大家:这道题目的答案是什么?
integral(8&4) y dy/(y^2-2y-3)
|
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-2-2014 08:06 AM
|
显示全部楼层
发表于 19-2-2014 08:06 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-2-2014 08:53 AM
|
显示全部楼层
mathlim 发表于 19-2-2014 08:06 AM 
看不懂题目!
8&4 是什么?
就是那个符号的下面是4上面是8。
|
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-2-2014 09:00 PM
|
显示全部楼层
发表于 19-2-2014 09:00 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-2-2014 10:21 PM
|
显示全部楼层
weitao 发表于 19-2-2014 09:00 PM 
LZ,我不明白8&4
就是S(上面是8下面是4)
|
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-2-2014 12:24 AM
|
显示全部楼层
发表于 20-2-2014 12:24 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-2-2014 10:38 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-2-2014 05:59 PM
|
显示全部楼层
发表于 20-2-2014 05:59 PM
|
显示全部楼层
太久沒玩integration了。。我嘗試回答。應該是用integration by parts解決。
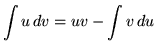
Let u = y; du/dy = 1;
dv/dy = 1/(y^2-2y-3) = 1/(y-3)(y+1)
now we have to integrate dv.
1/(y^2-2y-3) = 1/(y-3)(y+1)
把兩個分母拆開
1/(y-3)(y+1) = A/(y+1) + B/(y-3) = 1
Let y = -1
so B = -1/4
Let y = 3
so A = 1/4
integrate of dv/dy = 1/4(y+1) - 1/4(y-3)
v = 1/4 { ln |y+ 1| - ln |y-3| }
Thus, integrate of
8 y dy
4 y^2-2y-3
= {y . 1/4 [ ln |y+ 1| - ln |y-3| ] } - [1/4 [ ln |y+ 1| - ln |y-3| ]
= { 8 . 1/4 [ ln 9/ln 5 ] - 4 . 1/4 [ ln 5/ln 1] } - 1/4 [ ln 9/ln 5 ] - 0
= 2 [ln 9/ln 5 ] - 1/4 [ ln 9/ln 5 ]
= 1 3/4 [ln 9/ln5]
本帖最后由 liang_2002 于 20-2-2014 06:04 PM 编辑
|
评分
-
查看全部评分
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-2-2014 12:54 PM
|
显示全部楼层
发表于 21-2-2014 12:54 PM
|
显示全部楼层
使用integration by partial fractions应该更快吧...
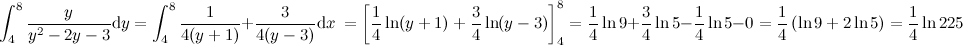
更正,第2个equation应该是dy而不是dx... 本帖最后由 ystiang 于 21-2-2014 01:03 PM 编辑
|
评分
-
查看全部评分
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|