多普勒的趣题分享 (11/11 新加题目)

多普勒效应

最近看到一些蛮有趣的比赛题目，放上来大家看看 ^^

2-9-07


答案是整数!

-------------------------------------------------------------------------------

2-9-07 （解答在 #35,#37）



-------------------------------------------------------------------------------

3-9-07
排列组合的~



-------------------------------------------------------------------------------

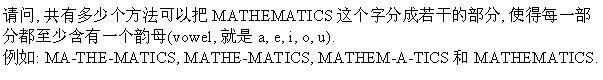
5-9-07
大家都看过世界杯:



-------------------------------------------------------------------------------

21-9-07

多普勒有五个盒子: 第一个盒子有: 2个正方形, 8个正三角形;
                  第二个盒子有: 3个正方形, 2个正三角形;
                  第三个盒子有: 3个正方形, 4个正三角形
                  第四个盒子有: 4个正方形, 3个正三角形;
                  第五个盒子有: 5个正方形, 4个正三角形.
已知每一个正三角形和正方形的边长都一样.
多普勒选了一个盒子,尝试用尽盒子里面的正方形和正三角形来组成一个完整的多面体(polyhedra).
请问,多普勒选中不可能组成多面体的盒子的概率是多少?

-------------------------------------------------------------------------------

4-10-07

现有 7 红球, 8 蓝球, 9青球.
请问, 有多少种选取 11 粒球的方法使得这11粒球中至少有 2 红球及 2 青球; 最多有 5 蓝球, 5 青球?

-------------------------------------------------------------------------------

10-10-07

多普勒有3个箱子, 各别有100粒球, 球上标上1 到 100的号码. (也就是说, 每一个箱子都有一set完整的表上1,2,..,100的球)
现在,我从三个箱子各别随机选取一个球(共得3球).
请问, 把三个球表面上的数字相加所得的数是119的概率为多少?

-------------------------------------------------------------------------------

11-11-07



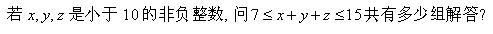
[ 本帖最后由 多普勒效应 于 10-11-2007 09:38 PM 编辑 ]

lyt87

是这样吗？

[ 本帖最后由 lyt87 于 2-9-2007 03:31 PM 编辑 ]

jhwong_alen

原帖由 多普勒效应 于 2-9-2007 02:00 PM 发表
最近看到一些蛮有趣的比赛题目，放上来大家看看 ^^

2-9-07


答案是整数!

答案是861 ?对吗？？

多普勒效应

原帖由 jhwong_alen 于 2-9-2007 03:46 PM 发表


答案是861 ?对吗？？

对对 ^^
请问你的解答是怎样的?

多普勒效应

原帖由 lyt87 于 2-9-2007 03:27 PM 发表
http://i15.wwwwwww.com/4zbxj81.gif


是这样吗？

lyt 兄, 我看不到你的解答

dunwan2tellu

我相信他可以一般化：

将点 P1 , P2 , ... , Pn 排列在一条线上，且符合条件 |Pi - P_(i+1)| = 1/i , 那么

任何两点之间的距离的和 = n(n-1)/2

jhwong_alen

原帖由 多普勒效应 于 2-9-2007 04:02 PM 发表


对对 ^^
请问你的解答是怎样的?

我是将解答的。。。
since |pi-pi+1|=1/i
as we know, p1<p2<p3<p4<....<p41<p42
hence,sum of any 2 point from
p1 to p2 is |p1-p2|=1
p1 to p3 is |p1-p2|+|p1-p3|+|p2-p3|=1+[3/2+1/2]=1+2
p1 to p4 is |p1-p2|+|p1-p3|+|p2-p3|+|p1-p4|+|p2+p4|+|p3-p4|=1+2+[1+1/2+1/3+1/2+1/3+1/3]=1+2+3
.
.
p1 to pn is 1+2+3+4+.....+(n-1)
sum of 2 point from p1 till p42 is 1+2+3+.....+41 is A.P. series
Sn=n/2 x[2a+(n-1)d]
a=1,n=41,d=1
S&#8324;&#8321;=41/2 x[2+40]
     =861

[ 本帖最后由 jhwong_alen 于 2-9-2007 07:17 PM 编辑 ]

dunwan2tellu

原帖由 jhwong_alen 于 2-9-2007 06:03 PM 发表


我是将解答的。。。
since |pi-pi+1|=1/i
as we know, p1

但是

|P2 - P3| = 1/2  而不是 2 .....

jhwong_alen

原帖由 dunwan2tellu 于 2-9-2007 06:27 PM 发表


但是

|P2 - P3| = 1/2  而不是 2 .....

sorry...用错方法解释。。
我编辑好了。。在帖#7。。那样应该没错了。。
可是你说画在直线上，那就有42个点，有 42C2=861 条线要算，要一条条画出来算是很麻烦的。。有没有更简单的方法作呢。。？

[ 本帖最后由 jhwong_alen 于 2-9-2007 07:19 PM 编辑 ]

dunwan2tellu

原帖由 jhwong_alen 于 2-9-2007 06:03 PM 发表


我是将解答的。。。
since |pi-pi+1|=1/i
as we know, p1

答案是“做”到了，不过却没有证明为什么

p1 to pn 的 total distance = 1 + 2 + 3 + ... + (n-1)

可以尝试用 数学归纳法

jhwong_alen

原帖由 dunwan2tellu 于 2-9-2007 07:17 PM 发表


答案是“做”到了，不过却没有证明为什么

p1 to pn 的 total distance = 1 + 2 + 3 + ... + (n-1)

可以尝试用 数学归纳法

数学归纳法？？是什么啊？/怎样用？？能教教一下吗？

jhwong_alen

原帖由 dunwan2tellu 于 2-9-2007 07:17 PM 发表


答案是“做”到了，不过却没有证明为什么

p1 to pn 的 total distance = 1 + 2 + 3 + ... + (n-1)

可以尝试用 数学归纳法

换另一个想法。。
   42
sum |p1-pi| =41+40(1/2)+39(1/3)+38(1/4)+.....+1(1/41)
  i=2
   42
sum |p2-pi| =40(1/2)+39(1/3)+38(1/4)+......+1(1/41)
  i=3
.
.
.
   42
sum |p40-pi| =  2(1/40)+1(1/41)
   i=41

    |p41-p42| = 1/41

hence,
sum of all = 41(1)+(2)(40)(1/2)+(3)(39)(1/3)+(4)(38)(1/4)+......(40)(2)(1/40)+(41)(1)(1/41)  
           = 41+40+39+38+....+2+1
           = 41/2 [42]
           = 861

多普勒效应

我的一般性的解答.

有错告诉我

[ 本帖最后由 多普勒效应 于 2-9-2007 09:49 PM 编辑 ]

多普勒效应

好的, 再来一题



这两题都是近年来的澳洲数学比赛赛题!

jhwong_alen

原帖由 多普勒效应 于 2-9-2007 09:38 PM 发表
好的, 再来一题



这两题都是近年来的澳洲数学比赛赛题!

不明白。。
什么是“两条对角线的交角”？？
正多边形是poligon 啊?

mathlim

27.将42个点P1,P2,P3,... ...,P42依序排在一直线上, 使得点Pi与点Pi+1之间的距离为1/i, 其中1 ≤ i ≤ 41. 请问这些点中所有两个点之间的距离的总和为多少?

我也解过这一道题，与大家分享吧！

P1—1/1—P2—1/2—P3—1/3—P4—1/4—P5—……—P40—1/40—P41—1/41—P42

红色的分数表示两个点之间的距离。
以下为每一段距离所需计算的次数。

1/1 : 1×41
1/2 : 2×40
1/3 : 3×39
1/4 : 4×38
...
1/40 : 40×2
1/41 : 41×1

这些点中所有两个点之间的距离的总和为
1×41×1/1 + 2×40×1/2 + 3×39×1/3 + 4×38×1/4 + … … + 40×2×1/40 + 41×1×1/41
= 41 + 40 + 39 + 38 + … … + 2 + 1
= 41×42 / 2
= 861

让我来说明一下吧！
比如点P4与点P5之间的距离1/4.
P4的左边包括其本身共有4个点，
P5的右边包括其本身共有38个点。
所以一共有4×38段距离包含这一段距离，即
P1—P5, P1—P6, P1—P7, ……, P1—P41, P1—P42,
P2—P5, P2—P6, P2—P7, ……, P2—P41, P2—P42,
P3—P5, P3—P6, P3—P7, ……, P3—P41, P3—P42,
P4—P5, P4—P6, P4—P7, ……, P4—P41, P4—P42.

jhwong_alen

原帖由 多普勒效应 于 2-9-2007 09:14 PM 发表
我的一般性的解答.

有错告诉我

上面的部分还能理解。。。
到下面就不会了。。。
能解释那个总长度为什么是那样的formula，和怎样简化啊。。

hamilan911

原帖由 jhwong_alen 于 2-9-2007 11:05 PM 发表


上面的部分还能理解。。。
到下面就不会了。。。
能解释那个总长度为什么是那样的formula，和怎样简化啊。。

把他转换成factorial,然后simplify
多普勒的一般性解得很棒

多普勒效应

原帖由 jhwong_alen 于 2-9-2007 10:46 PM 发表


不明白。。
什么是“两条对角线的交角”？？
正多边形是poligon 啊?

嗯, 例如下图:

角AXC就是对角线AD和CF的交角 ^^

正多边形是regular poligon.
就是每个边的长度都一样的poligon  

多普勒效应

原帖由 mathlim 于 2-9-2007 11:04 PM 发表
27.将42个点P1,P2,P3,... ...,P42依序排在一直线上, 使得点Pi与点Pi+1之间的距离为1/i, 其中1 ≤ i ≤ 41. 请问这些点中所有两个点之间的距离的总和为多少?

我也解过这一道题，与大家分享吧！:l ...

mathlim兄的解答很清楚噢!

原帖由 jhwong_alen 于 2-9-2007 11:05 PM 发表


上面的部分还能理解。。。
到下面就不会了。。。
能解释那个总长度为什么是那样的formula，和怎样简化啊。。

最下面那行, 就其实是算每个线段被"用"了多少次.
应该和mathlim兄的差不多!

[ 本帖最后由 多普勒效应 于 3-9-2007 09:27 AM 编辑 ]